※このウェブページは中学校理科1年の学習内容です。<1年p.59>
理路整然 どうする,本当の値はわからない
私たちは,ものさしで物体の長さをはかったり,てんびんで物体の質量をはかったりします。実はこのとき,真の値(本当の値)はわかりません。測定器の精度や,人による計器の読み取りの精度など,いろいろな原因によって,測定値には不正確さが入ってきます。測定値と真の値の差を誤差といいます。
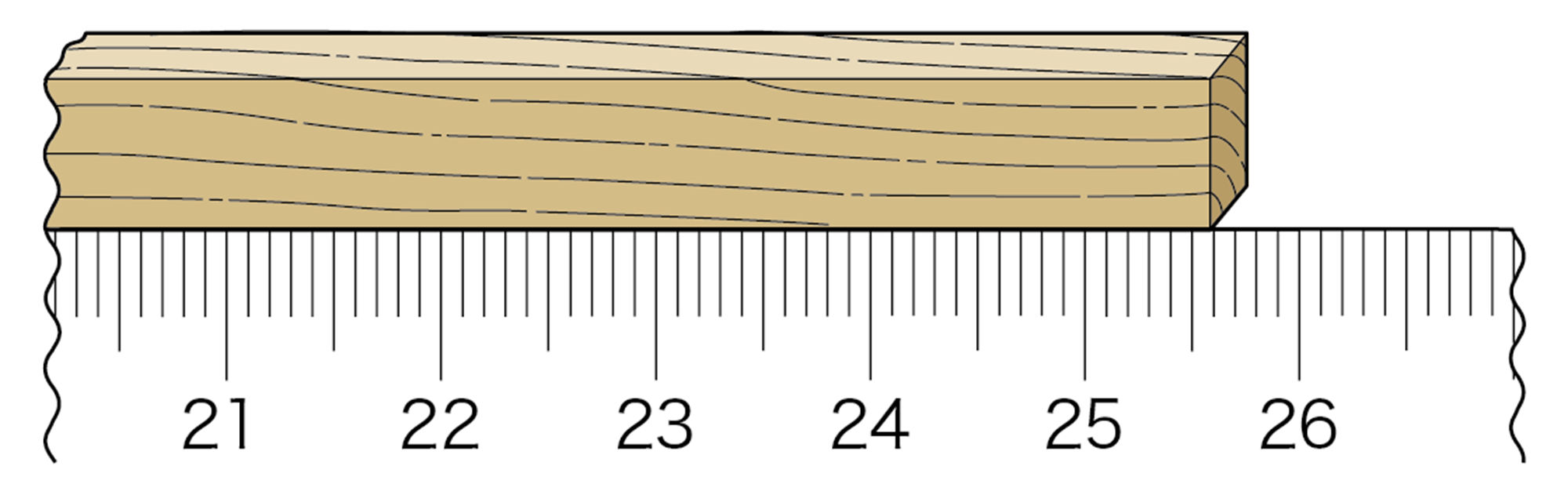
理科では,目盛りの読み方として「最小目盛りの1/10まで数値を読み取る」と決めています。たとえば1.mm目盛りのものさしで,図のように木材の長さをはかり,255.8.mmという測定値を得たとしましょう。255.8という測定値は,ものさしの目盛りを読み取って得た有意義な数字とされ,これを有効数字といいます。この場合,有効数字は4桁けたであるといい,最後の「8」という数字には,目分量で読み取った誤差がふくまれることになります。
有効数字は桁数で表現します。たとえば,ある棒の長さをcmの単位まではかり,350.cmという測定値を得たとします。この測定値をm単位で表し,かつ有効数字が3桁であることを示したいときは,3.50.mと書きます。
たとえば,教科書の厚さや質量をはかって,みんなで比べてみましょう。同じ本なので,同じになるはず?

発展
1/10.秒まではかれる時計で,ある人が.100m.を走る時間をはかったら,14.0.秒であったとする。このときの有効数字は3桁である。また,このときの速さは
100m÷14.0s=7.1428…m/s
となり,計算上は,いくらでも細かく求められることになる。
ここで,14.0という計測値は,14.05未満,13.95以上を意味する。そうすると,速さの上限と下限は,
100m÷14.0499…s=7.117…m/s
100m÷13.950…s=7.168…m/s
となり,商の3桁目に差が出てくる。商の上限と下限を考慮して平均を求めると,
(7.117…+7.168…)÷2=7.1425…
となる。つまり3桁目は「4」を基準として,その上下2程度の幅がある。ただし,幅があるものの「4」は十分目安になる。これをふまえて,測定値の有効数字が3桁だった場合,計算結果の有効数字も3桁までとするのが一般的である。細かく計算できるからといって,多くの桁を示すことに意味があるとは限らないのである。
さらに深めれば,距離も100mちょうどとは限らない。このように,測定値を用いた計算をするときは,「常に有効数字を考えておくこと」「測定値には常に誤差があること」などを意識する必要がある。