gkt-horizontal-line
※このウェブページは中学校理科1年の学習内容です。<1年p.135>
理路整然 どうする,グラフの見極め

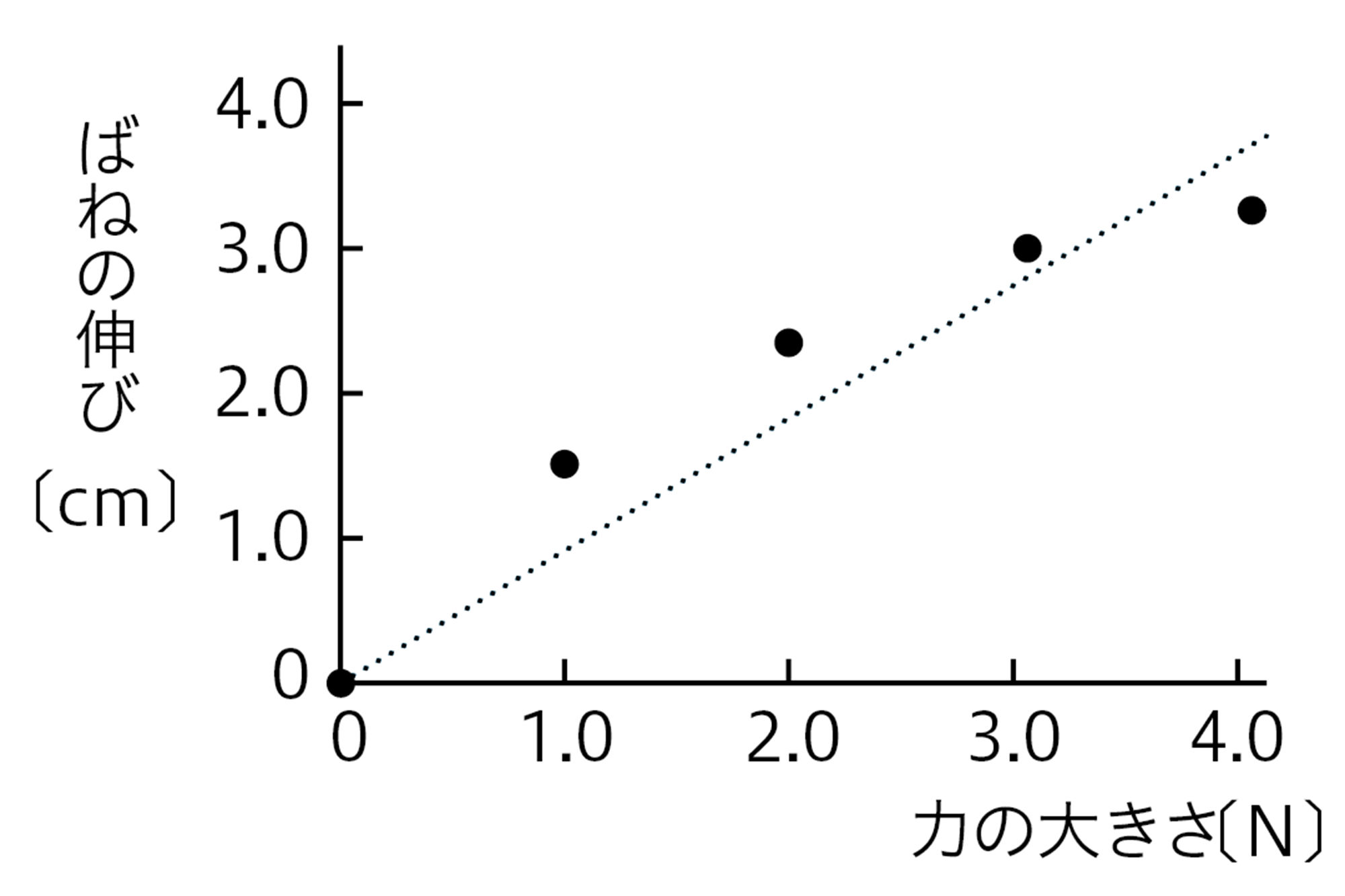
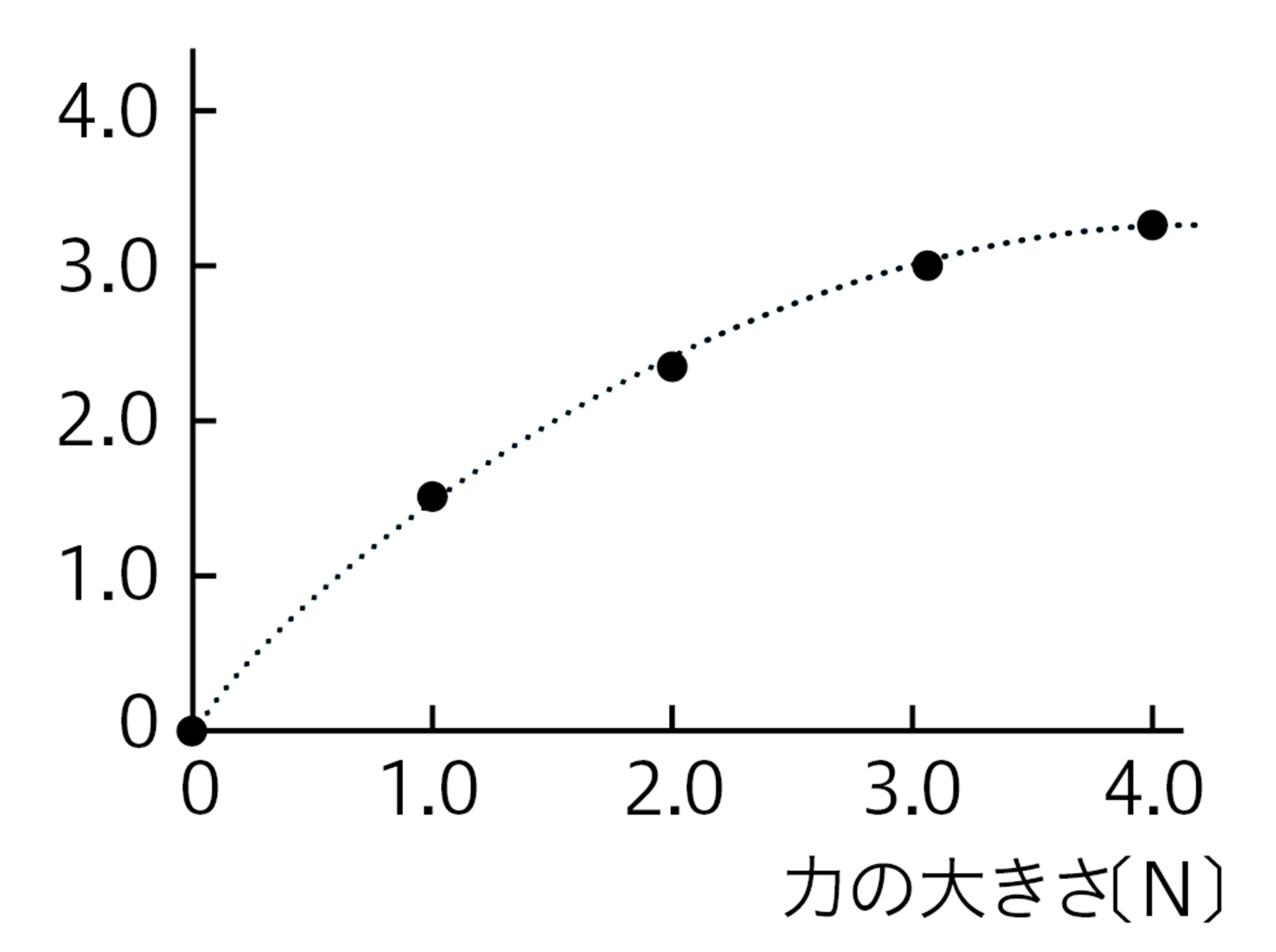
測定値の分布から,グラフは直線だと考えました。原点は通りませんでした。
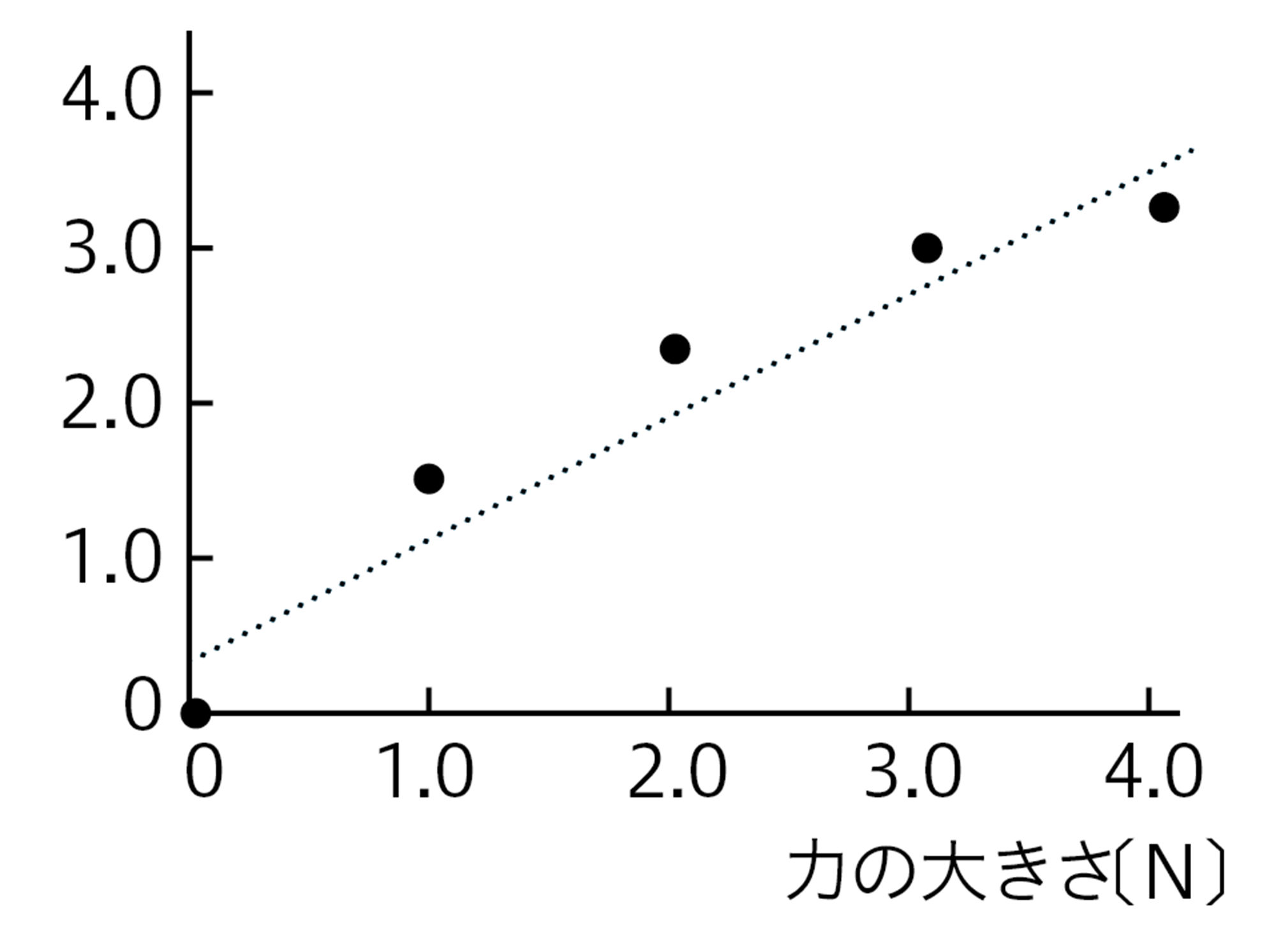
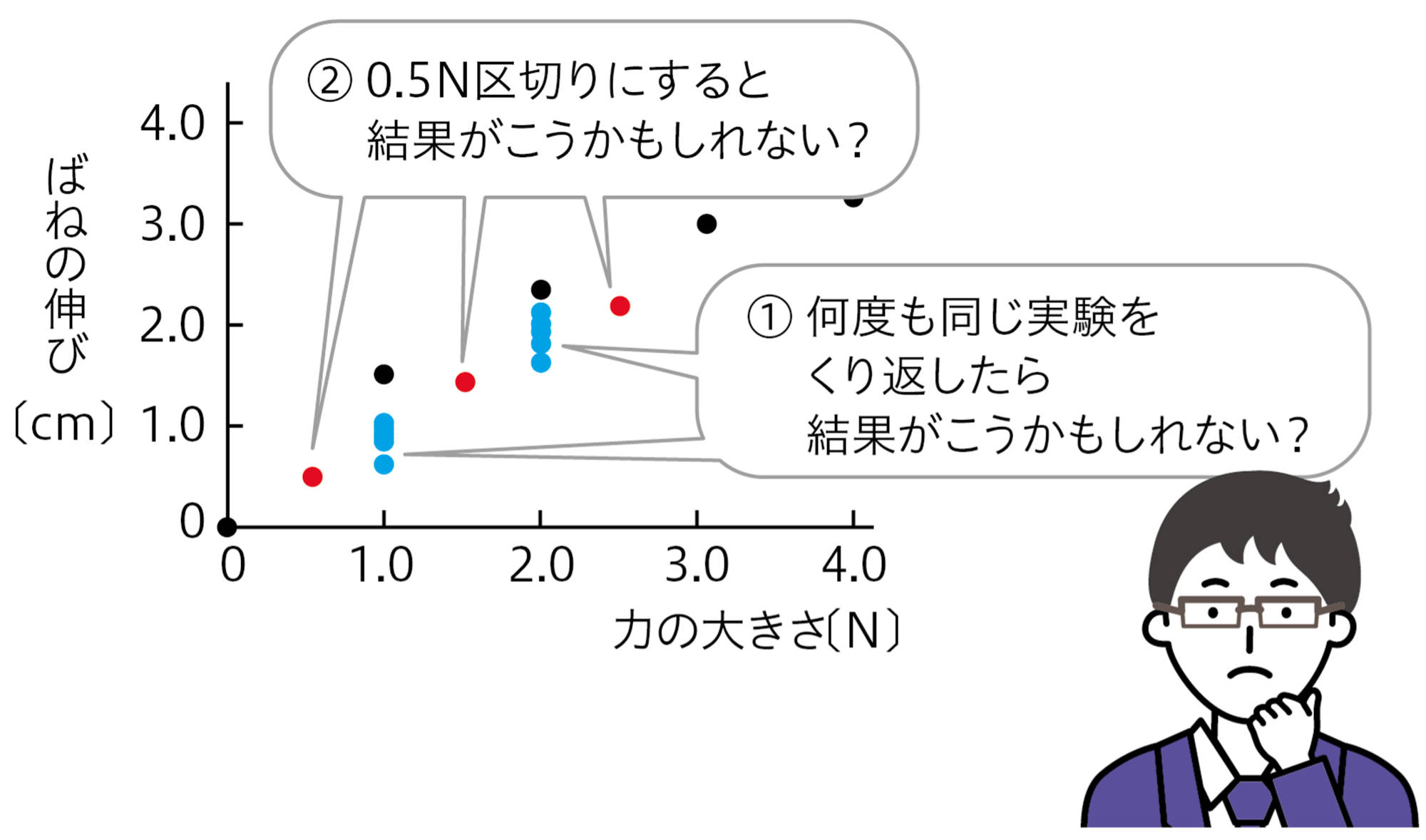
この探究では,力の大きさ,ばねの伸びといった結果の数値が得られます。その結果をもとにグラフ上に印を記入する(→p.214)のは,事実の範はん囲いです。印を記入するときに,人によるちがいはないからです。しかし,印の集まりを見て「どのような傾けい向こうがあるか」「どのような直線・曲線をえがくか」を考えるのは,「考察」であり,人によってちがうことがあります。
上の3人の例では,「おもりの数」と「ばねの伸び」にどのような関係があるか,意見が分かれました。3人のうち,だれが適切なのでしょうか。解決する方法のひとつは,結果を増やすことです。たとえば,同じ実験をくり返して結果を増やしていけば,同じ1.0Nの結果でも,数値にどのくらいのばらつきがあるか認識しやすくなり(下図①),傾向がはっきりするかもしれません。
あるいは,横よこ軸じくを,1.0N区切りから0.5N区切りと細かくして実験しなおすことも考えられます。すると,1.0N区切りのときにわかった結果の間をおぎなう数値がわかります(下図②)。このようにして,結果を増やすことで精度を上げ,傾向をつかみやすくするとよいでしょう。