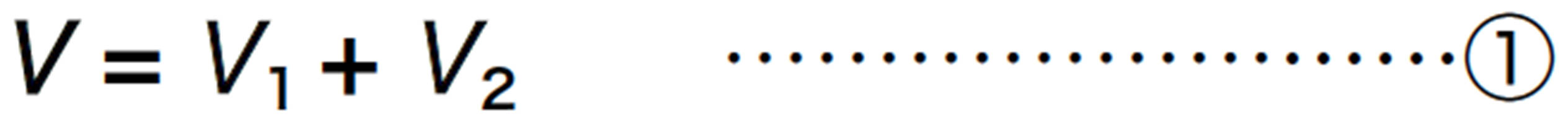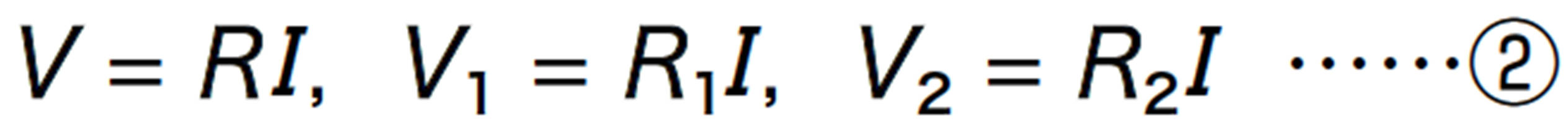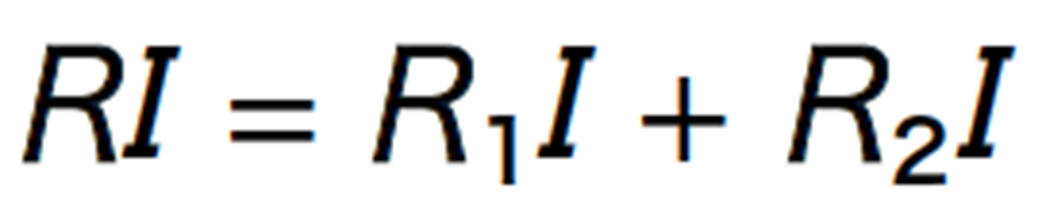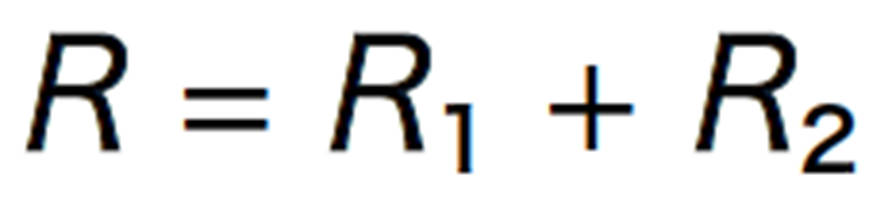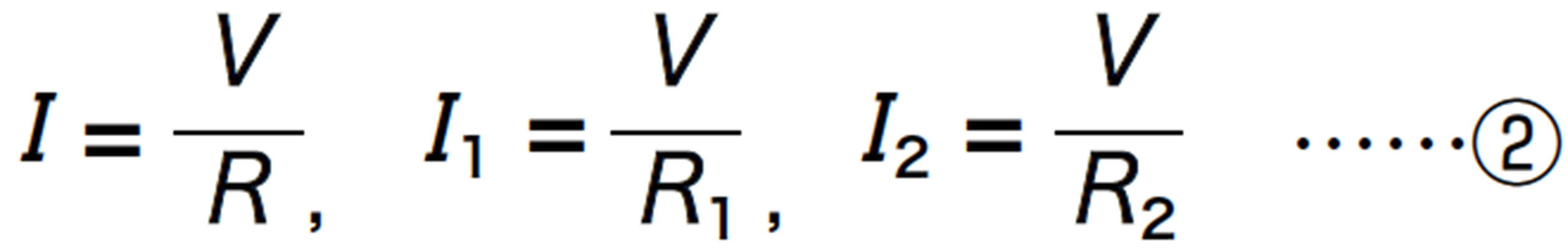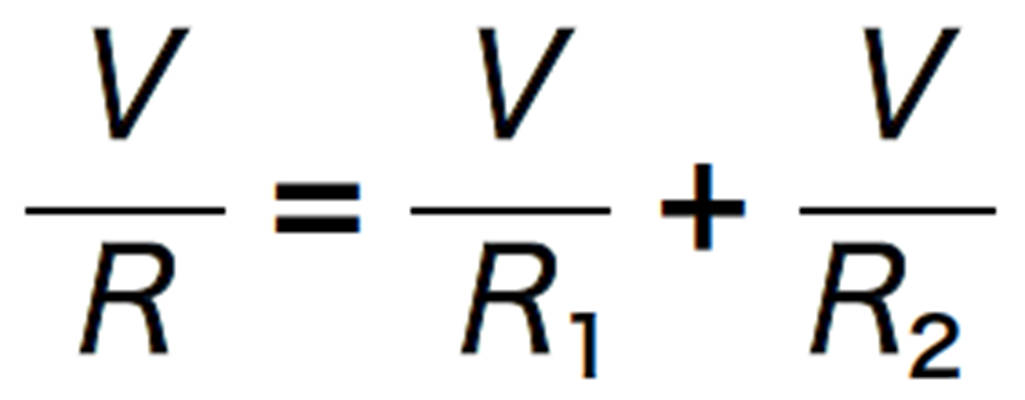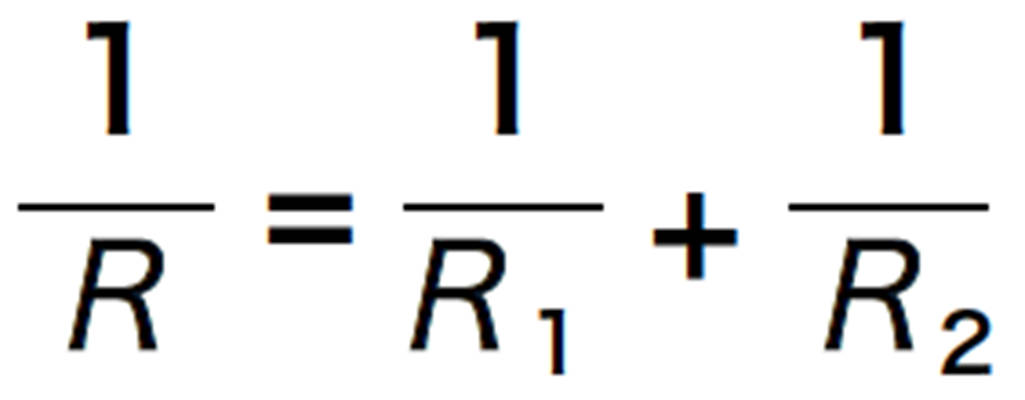※このウェブページは中学校理科2年の学習内容です。<2年p.147>
４ 直列・並列回路の抵抗
探究3の「実験A」２つの抵抗器の直列回路の結果（表2（a））と，「実験B」２つの抵抗器の並列回路の結果（表2（b））を比べる。すると，どちらも電源の電圧は同じ約3.0Vであるのに対して，直列回路の導線Z 点の電流は約90mA であり，並列回路の導線z 点の電流は約400mAと，異なっている。つまり，電源の電圧が同じで，同じく２種類の抵抗器を使っていても，抵抗器のつなぎ方によって，回路全体の電流の流れやすさが変わる（回路全体の抵抗が変わる）ことがわかる（図19）。
注意!! テスターで抵抗をはかるときは，電流を流さないようにする。
テスター（抵抗などをはかる機器）で，抵抗器の直列回路(a) と，並列回路(b) の全体の抵抗をはかった場合。端子とクリップをつないだ部分などに抵抗が発生し，実際の抵抗の値は理想的な値より高めになる。
図19 全体の抵抗と個々の抵抗
直列回路にかかる電圧の関係
オームの法則より，
②を①に代入すると，
両辺を \(\displaystyle I\) で割ると，
並列つなぎにすると，電流の流れる道筋が増えて流れやすくなり，合成抵抗は，ひとつひとつの抵抗よりも小さくなります。
R＜R₁，R＜R₂
並列回路を流れる電流の関係
オームの法則より，
②を①に代入すると，
両辺を \(\displaystyle V\)で割ると，
直列つなぎにすると，抵抗のあるところを長い距離流れるので，合成抵抗は，ひとつひとつの抵抗よりも大きくなります。
R＞R₁，R＞R₂
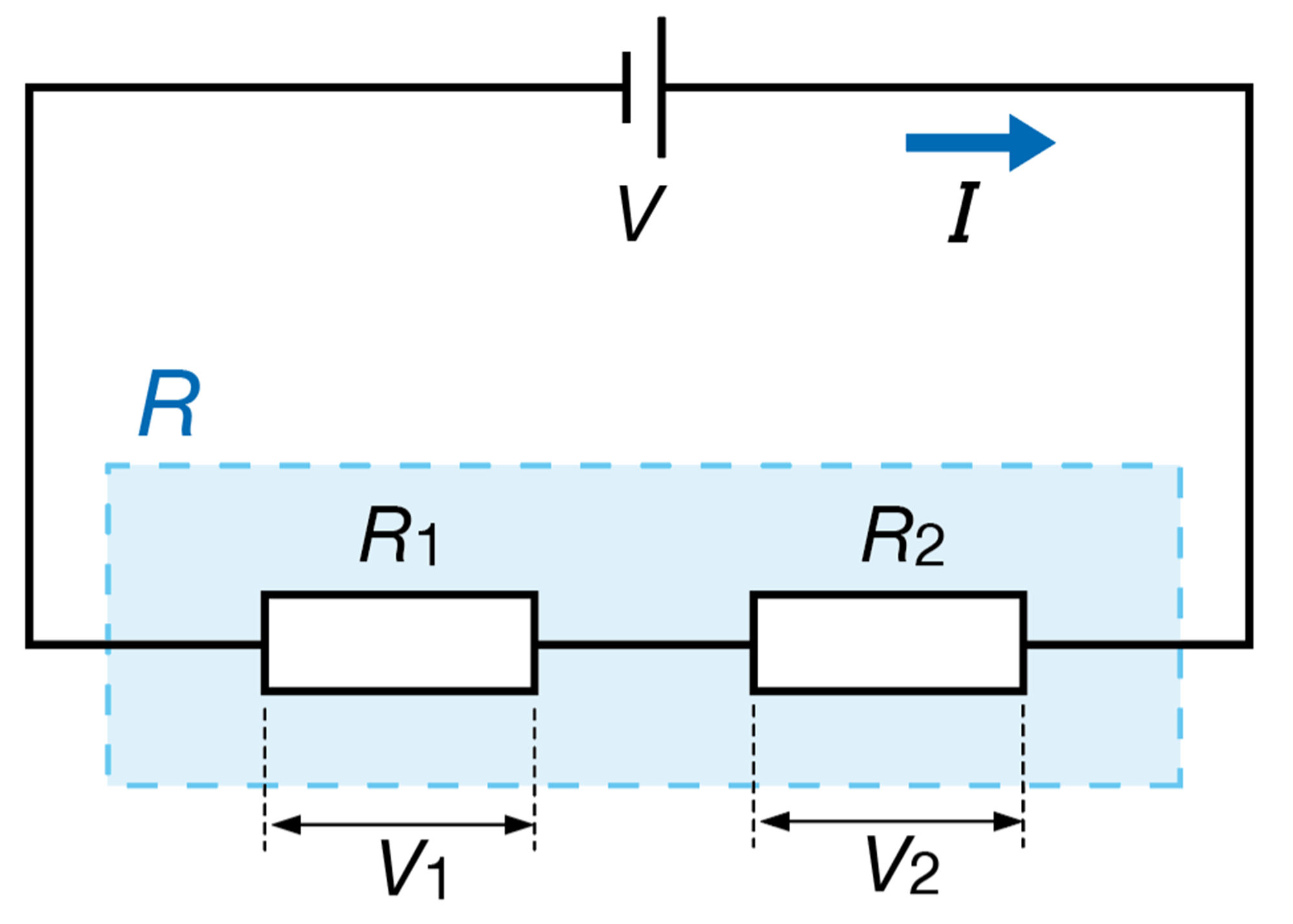
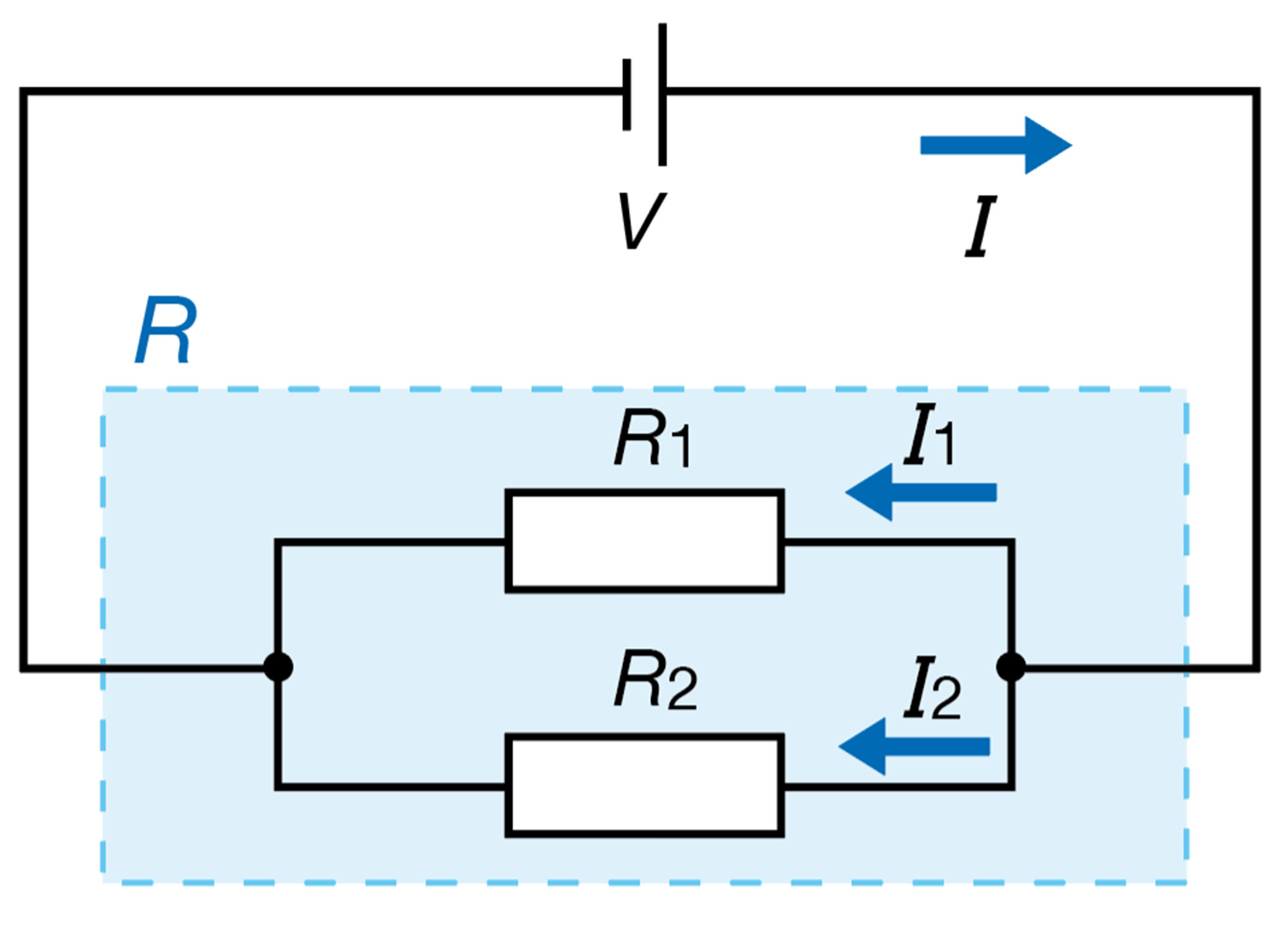
複数の抵抗器をつないだときの全体の電気抵抗の大きさを合成抵抗という。また，2 つの抵抗器を並列または直列につないだときは，２つの抵抗器R 1，R 2をまとめた全体の抵抗R という考え方ができる。そのとき全体の抵抗と，個々の抵抗の関係は上図のように求めることができる。
図20 合成抵抗の考え方