※このウェブページは中学校理科3年の学習内容です。<3年p.16>
２｜力の合成・分解
１ 一直線上にある2力の合成
水中の物体の浮き沈みは，浮力と重力の２力がつり合わず，上向き，または下向きの力が発生することで起こる。1つの物体が2力を受けているとき，この2力は，同じはたらきをする1つの力におきかえることができる。2力を1つの力におきかえることを力の合成といい，合成された力を合力という。
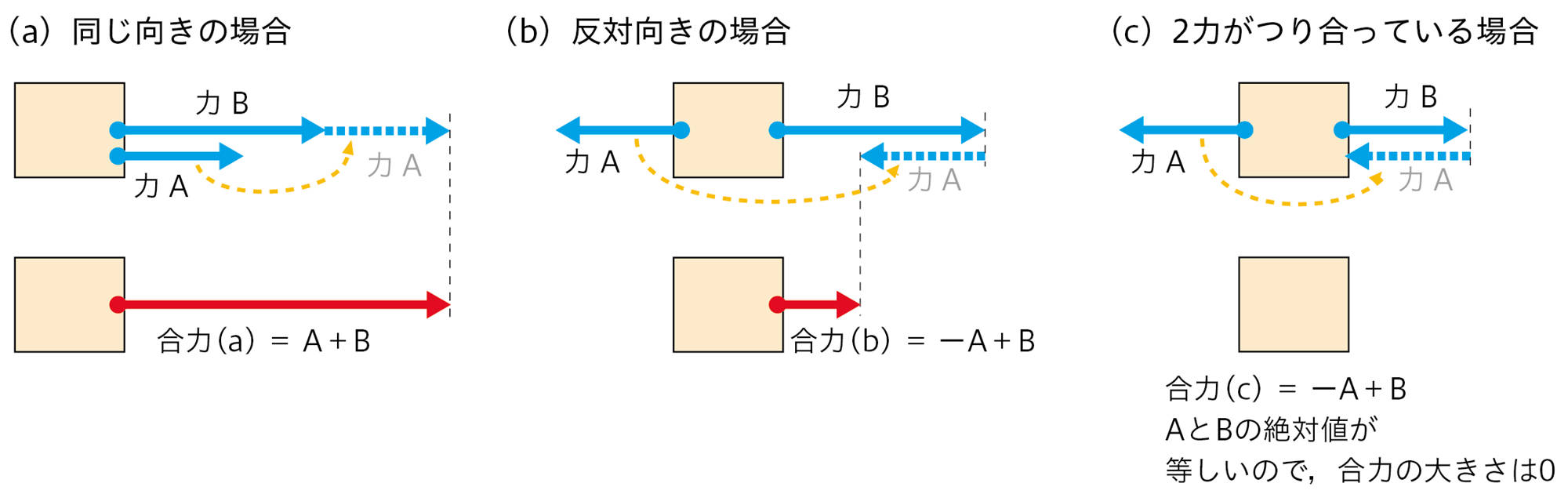
2力が一直線上にあり，同じ向きの場合は，合力の大きさは2力の和になる（図11(a））。逆に，2力が一直線上にあり，反対向きの場合は，合力の大きさは2力の差になる（b）。特に，2力がつり合っている場合は，合力の大きさは0である（c）。
図中の「合力」は(a)，(b)，(c)それぞれの場合の合力の大きさとする。「A」，「B」はそれぞれ力Aと力Bの力の大きさとする。
図11 一直線上にある２力の合力を調べる
（b）のように向きが反対の力は，数直線の正と負で考えるといいね。１年生の数学で学んだね。
1年生の理科で学んだ「２力がつり合って物体が動かないとき」というのは（c）のことだね。
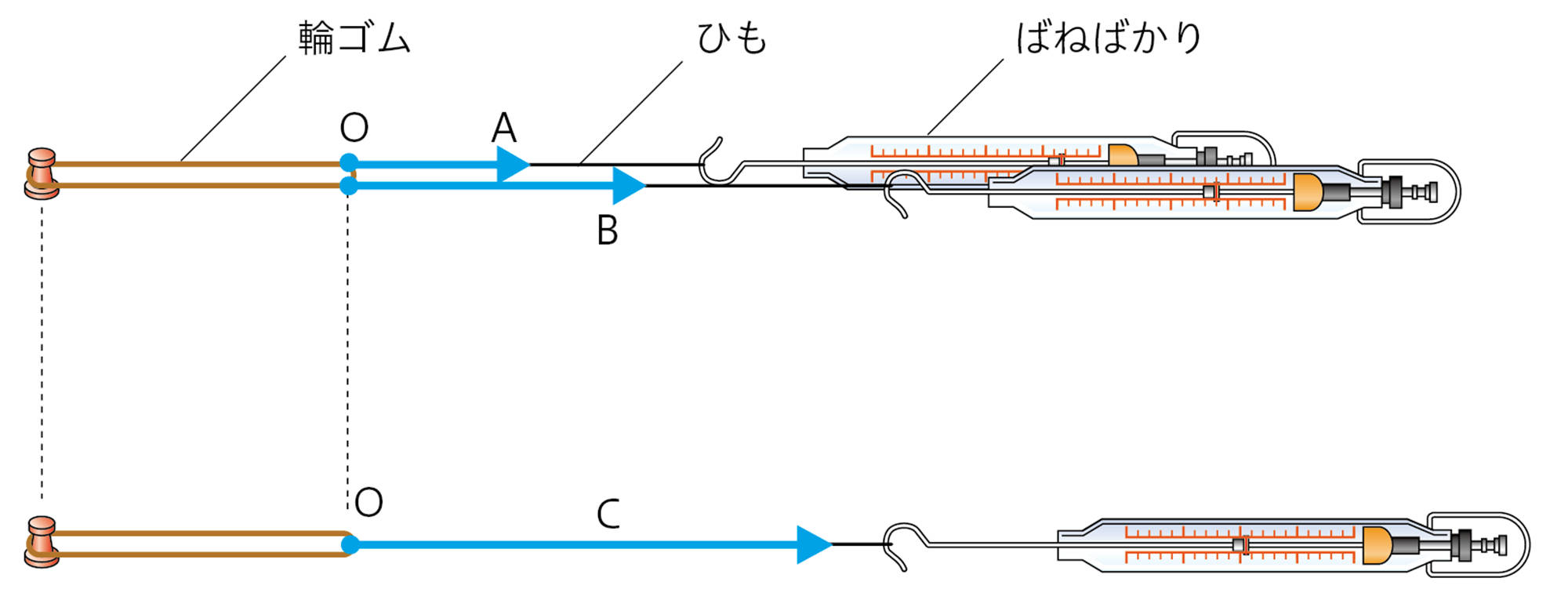
① 2つのばねばかりで，力の大きさが異なるようにして，同じ方向に輪ゴムを引く。伸ばした輪ゴムの端をO点として印をつけ，2つのばねばかりの示す力A，Bの大きさを調べる。
② 1つのばねばかりで輪ゴムを引き，①と同じO点まで伸ばして，力Cを調べる。
※このウェブページは中学校理科3年の学習内容です。<3年p.17>
２ 一直線上にない2力の合成
図11で，2力は一直線上にあるとき（2力のなす角が180°のとき）だけを考えていたが，実際は，一直線上にあるとは限らない。それ以外の角度の2力の合力について，どのように科学的に探究できるだろうか。
探究３ いろいろな向きの2力の合力
二人が荷物を持ったら，２力は一直線上にないよね。それでも２力の合力は計算できるのかな？
２力の角度が大きくなると，合力は大きくなる？小さくなる？
２力の向きや大きさがさまざまでも，決まった方法で合力が求められるのかな。
図13 物体を二人で左右から持つ
２力が一直線上にない場合，力はどのように合成されるか。
真上に力がはたらくと考えると，真上に足せばいいのかな？
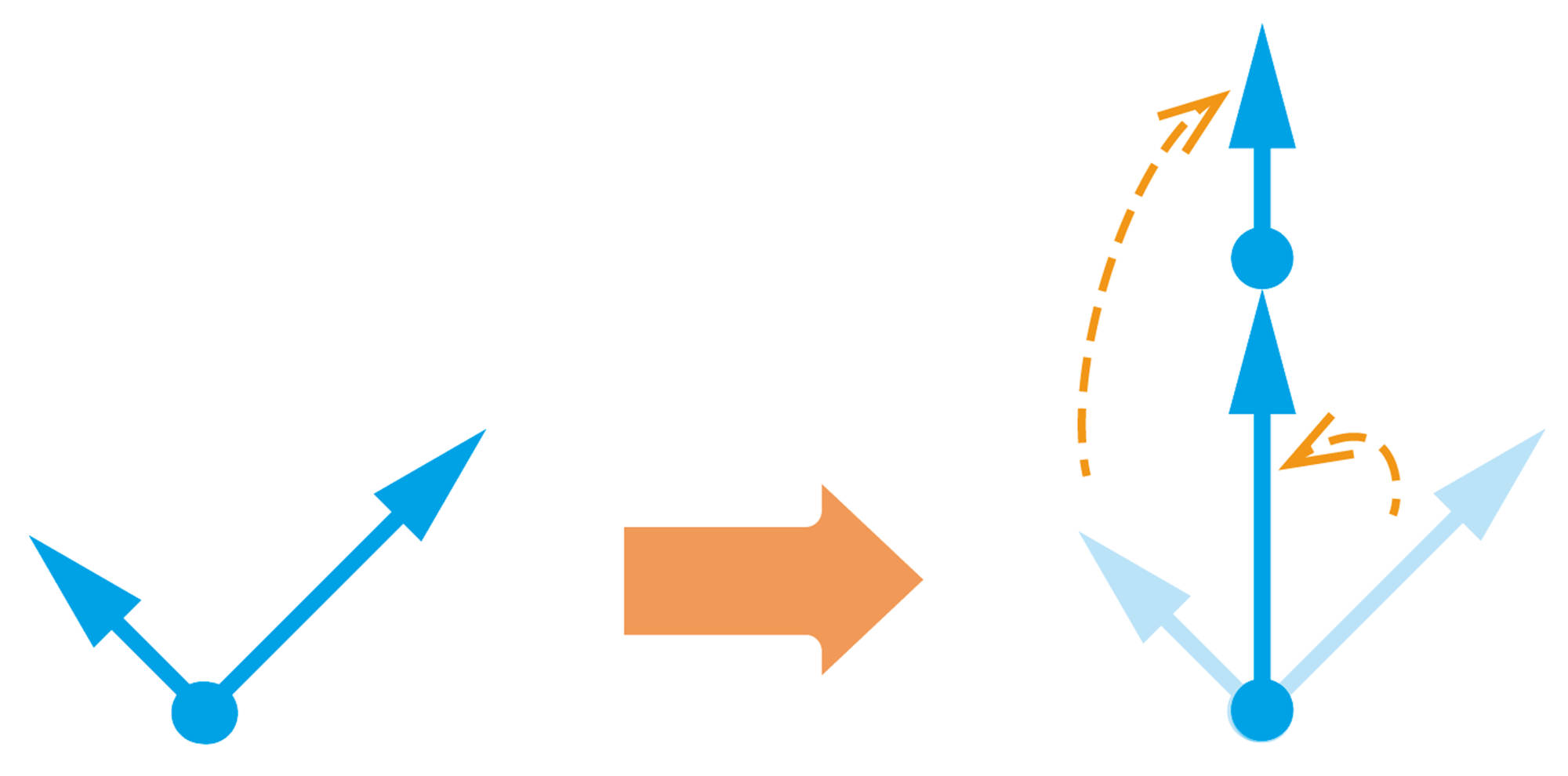
それでいいのかな？角度が大きい場合は横にひっぱってしまうし，そんなに力が出ないんじゃない？
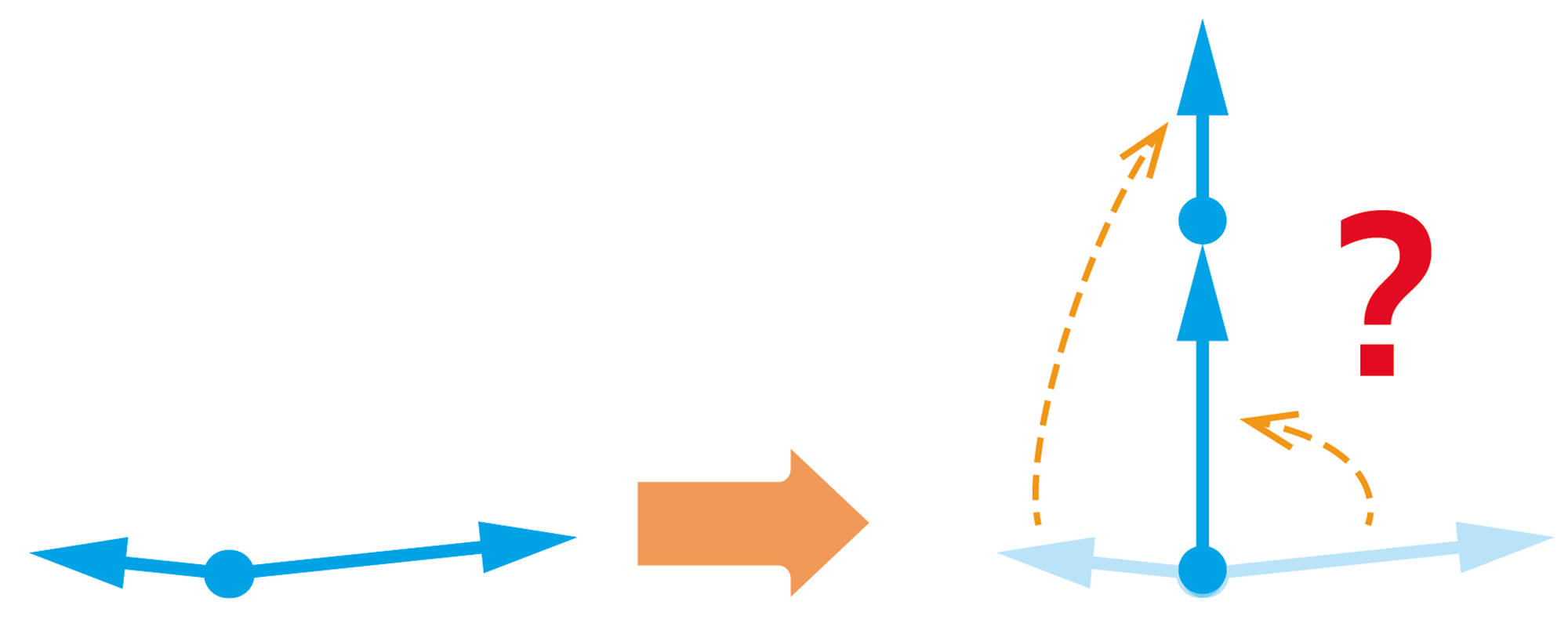
図12の方法が参考になりそう。
じゃあ，こうやってみたらどうだろう。
そのとき２力の合力はどうやってはかればいいだろう。
※このウェブページは中学校理科3年の学習内容です。<3年p.18>
この実験では，どのようにして合力を求めようとしているのかな?
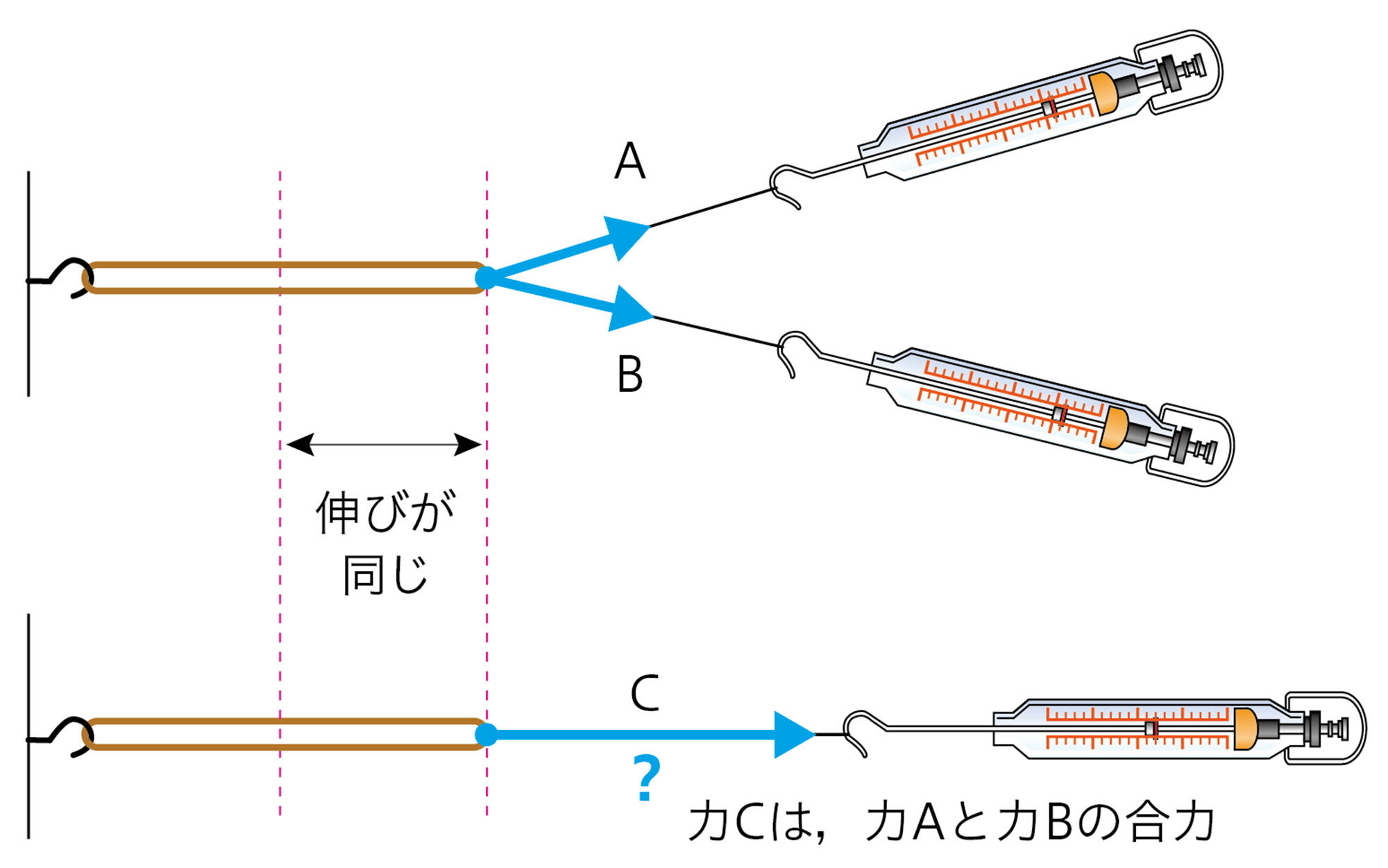
2力A，Bでゴムを伸ばします。次に，ゴムをまったく同じように伸ばす1つの力Cを見つけます。このときの力Cが2力の合力です。
２力A，Bと力Cのゴムの伸びが同じになるようにするんだね。
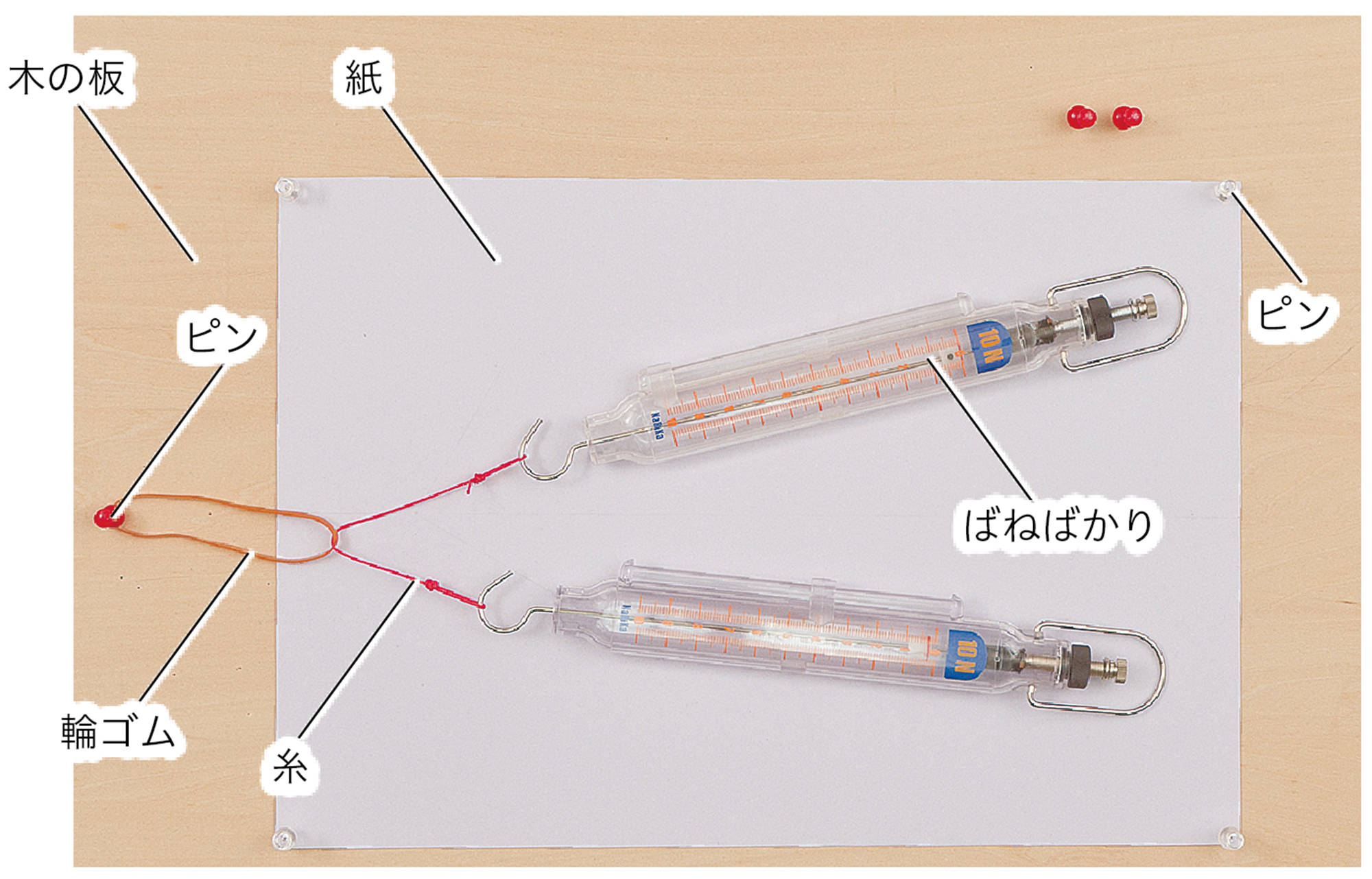
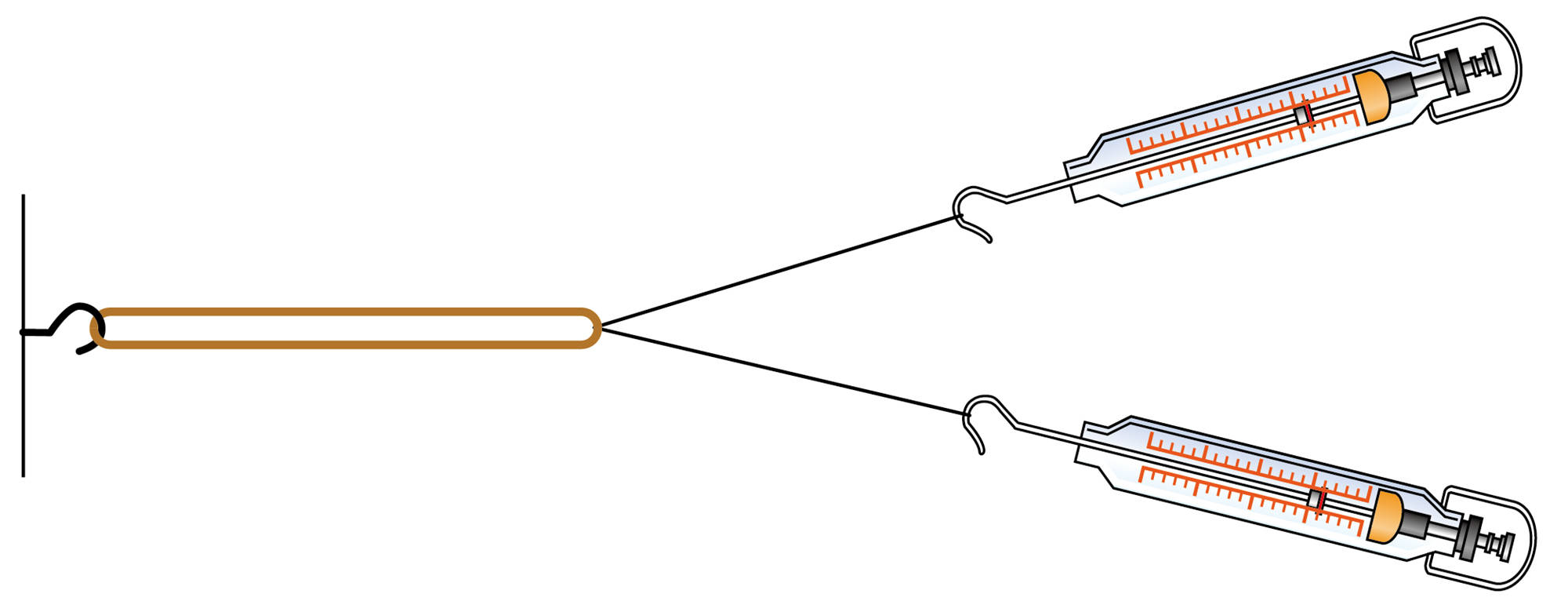
準備
ばねばかり（2），輪ゴム，糸，白い紙，木の板，ピン，分度器，ものさし，三角定規
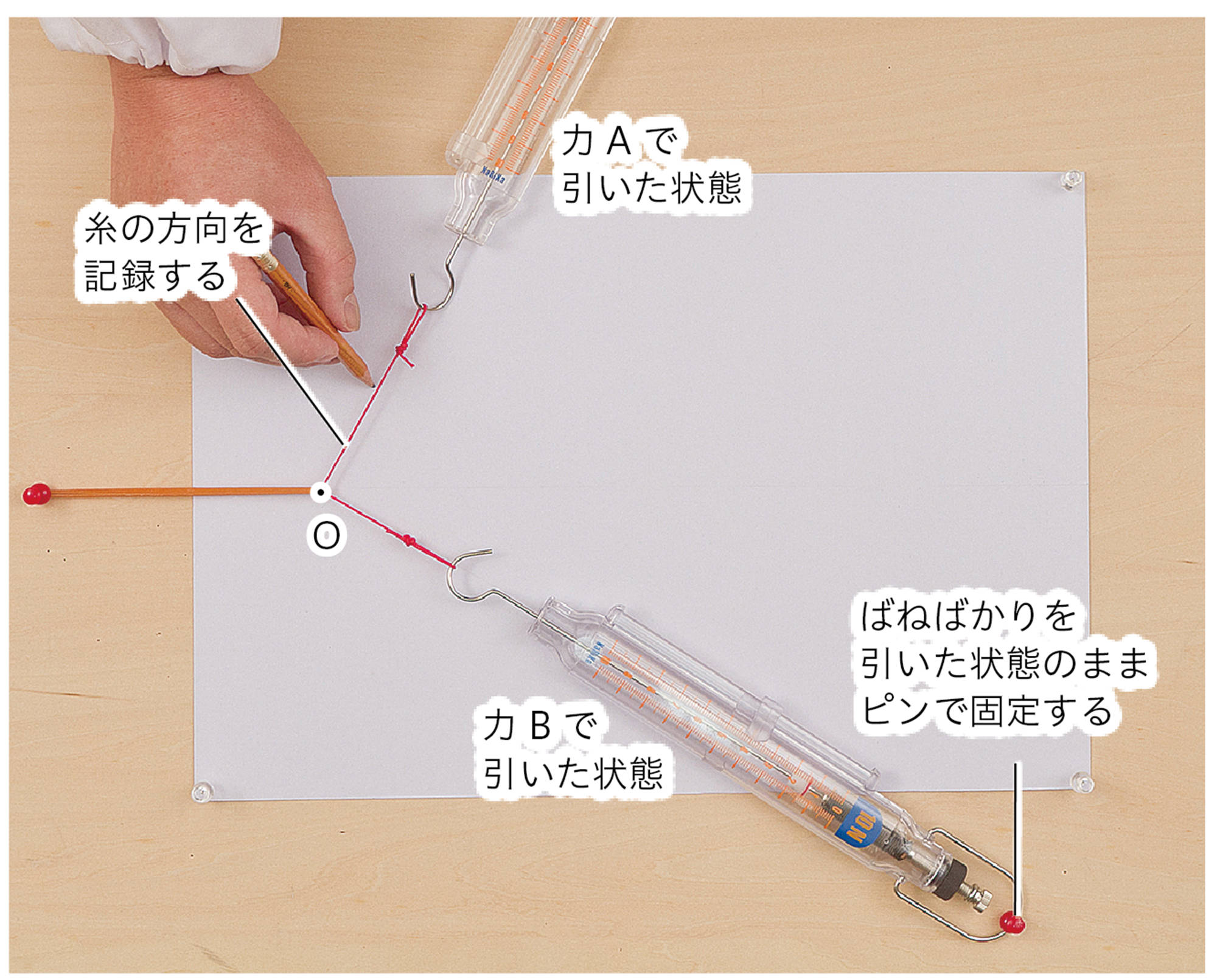
１．準備をする
木の板に白い紙をはり，輪ゴムの片方の端を板にさしたピンにかける。輪ゴムのもう片方の端に糸を取りつけ，それぞれの糸を2つのばねばかりで引けるようにつなぐ。
ポイント
ばねばかりは，水平にしたときに針が0を指すように調整しておく。
２．力Aと力Bで輪ゴムを伸ばす
2つのばねばかりを異なる方向に引いて，輪ゴムをある程度伸ばし，ばねばかりをピンで固定する。
このとき，２力のなす角度，２力の大きさは，班ごとにばらばらになるようにする。
① 伸びた輪ゴムの端をO点として紙に印をつけ，2本の糸の方向をうつしとる。
② 2つのばねばかりの示す力A，力Bの大きさを記録する。
※このウェブページは中学校理科3年の学習内容です。<3年p.19>
３．力Cで輪ゴムを同じ長さに伸ばす
ばねばかりを1つ取りはずし，1つの力を輪ゴムに加えて，2.と同じO点まで引き伸ばす。
① 糸の方向を紙にうつしとる。
② ばねばかりの示す力Cの大きさを記録する。
ポイント
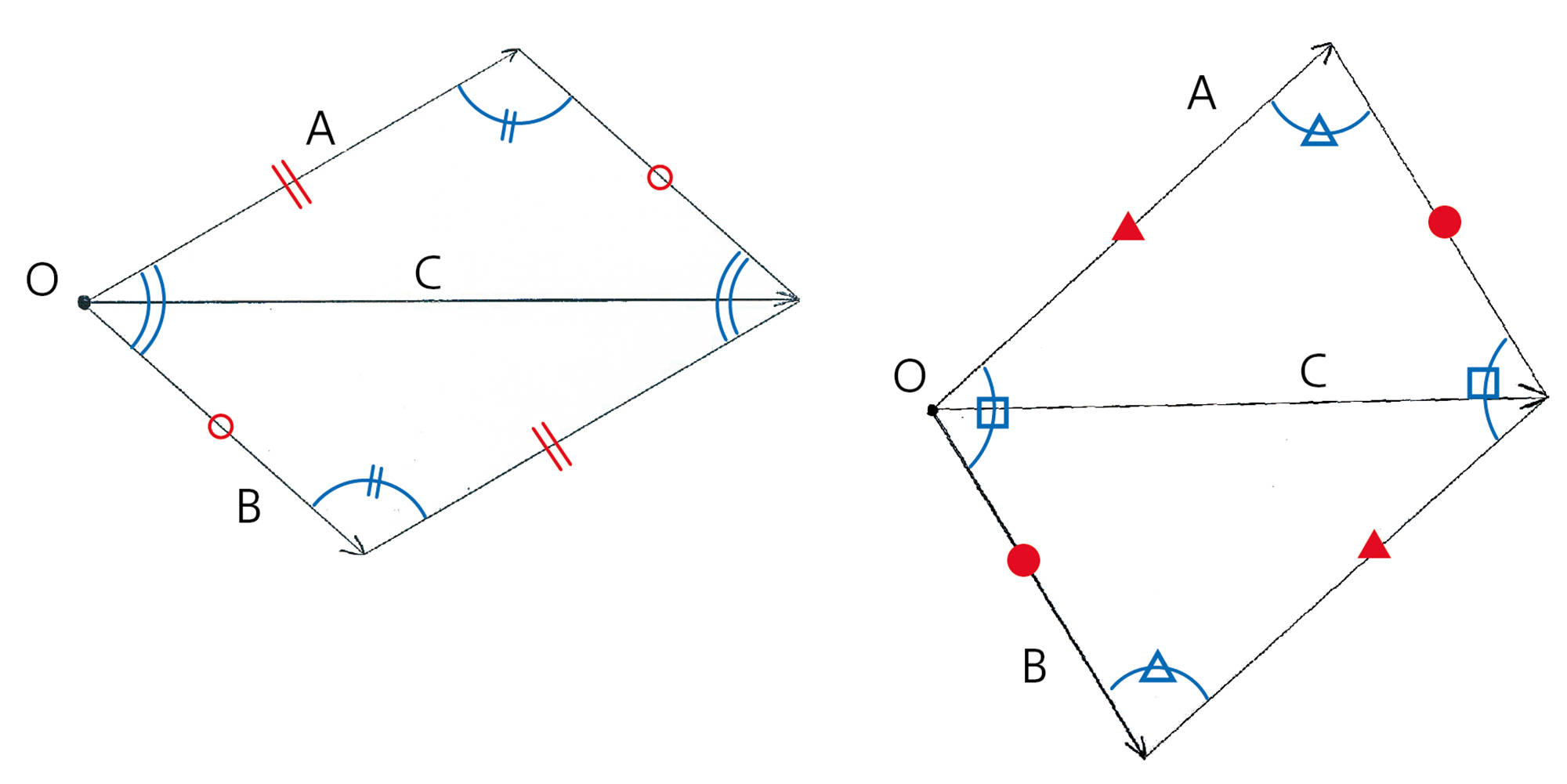
力A・B・Cを力の矢印で表す。
矢印の向き……記録した紙のO点から，それぞれの糸の向きにかく。
矢印の長さ……たとえば，0.1Nを1cmと決め，力の大きさに比例した長さにかく。
ポイント
各班で求めた力A・B・Cの関係から，どのような決まりがわかるか。
２辺の間の角や辺の長さを調べて，平行四辺形になっているか確かめましょう。
四角形ができたよ。平行四辺形のように見えるね。
力A，B，Cには，どのような関係があるといえるかな。
O，およびA，B，Cの矢印の先端がどのような関係にあるか注目しましょう。
平行四辺形の性質
・向かい合う辺が平行である。
・向かい合う辺の長さが等しい。（中学校2年）
※このウェブページは中学校理科3年の学習内容です。<3年p.20>
探究３ 結果から考察する
力A・B・Cの関係は右の図のようになる。
異なる方向に加えた2 力の合力は，それぞれの力の矢印をとなり合う2 辺とする平行四辺形の対角線となっていることがわかる。
※このウェブページは中学校理科3年の学習内容です。<3年p.21>
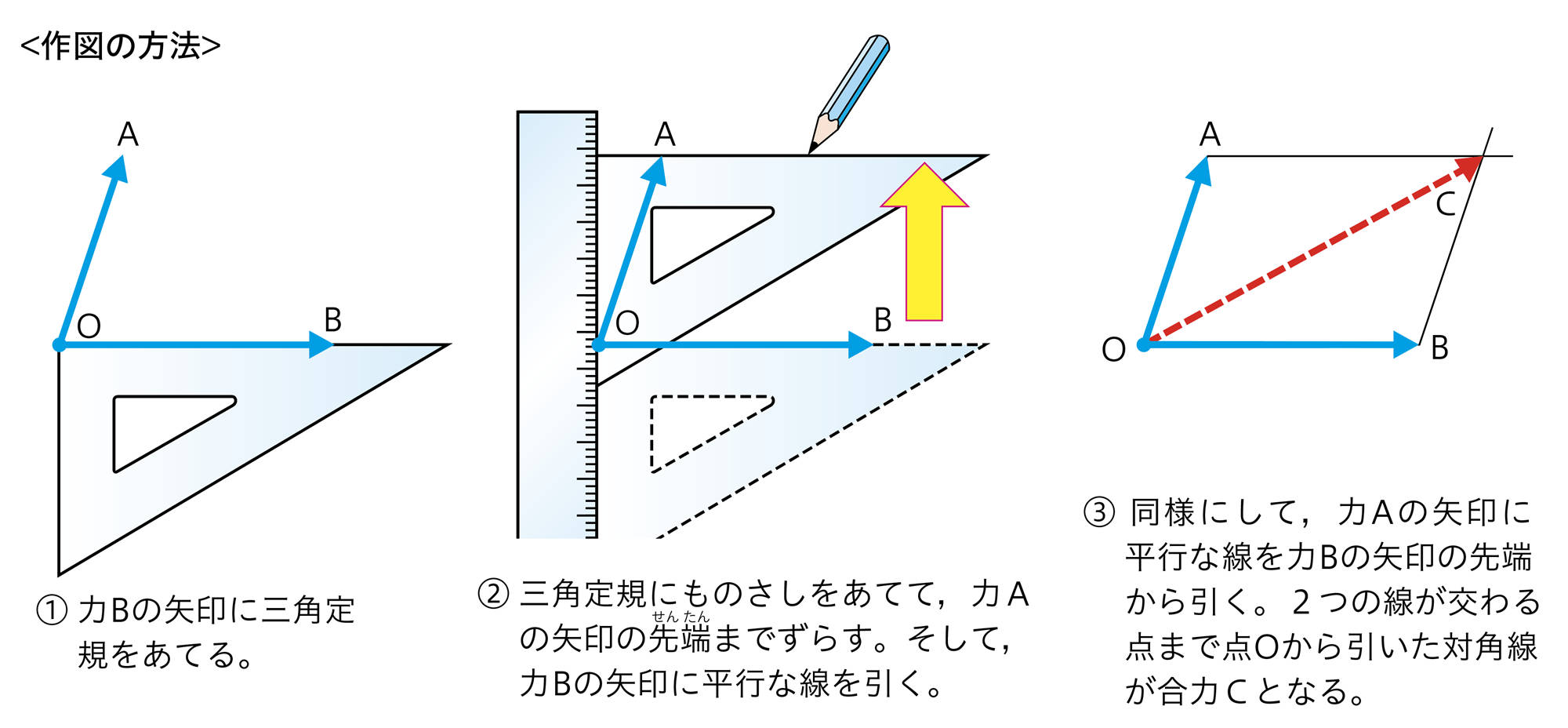
３ 力の合成
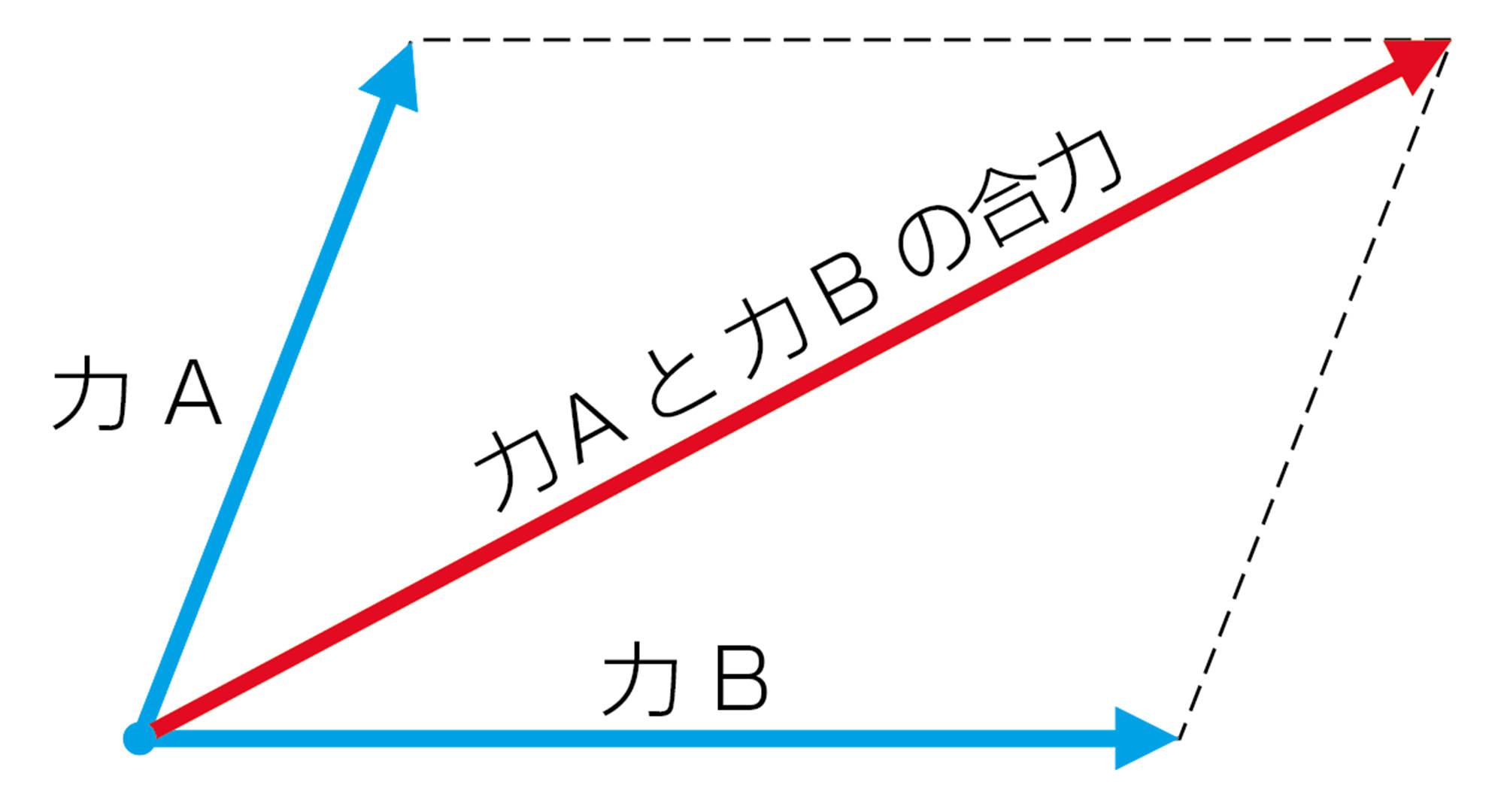
一般に物体が異なる方向の2力を受けるとき，その合力は，次の図のように2力の矢印を2辺とする平行四辺形の対角線を作図して求めることができる（図16）。
力Aと力Bの矢印を2辺とする平行四辺形をかき，その対角線を求めればよい。
図16 力の合成
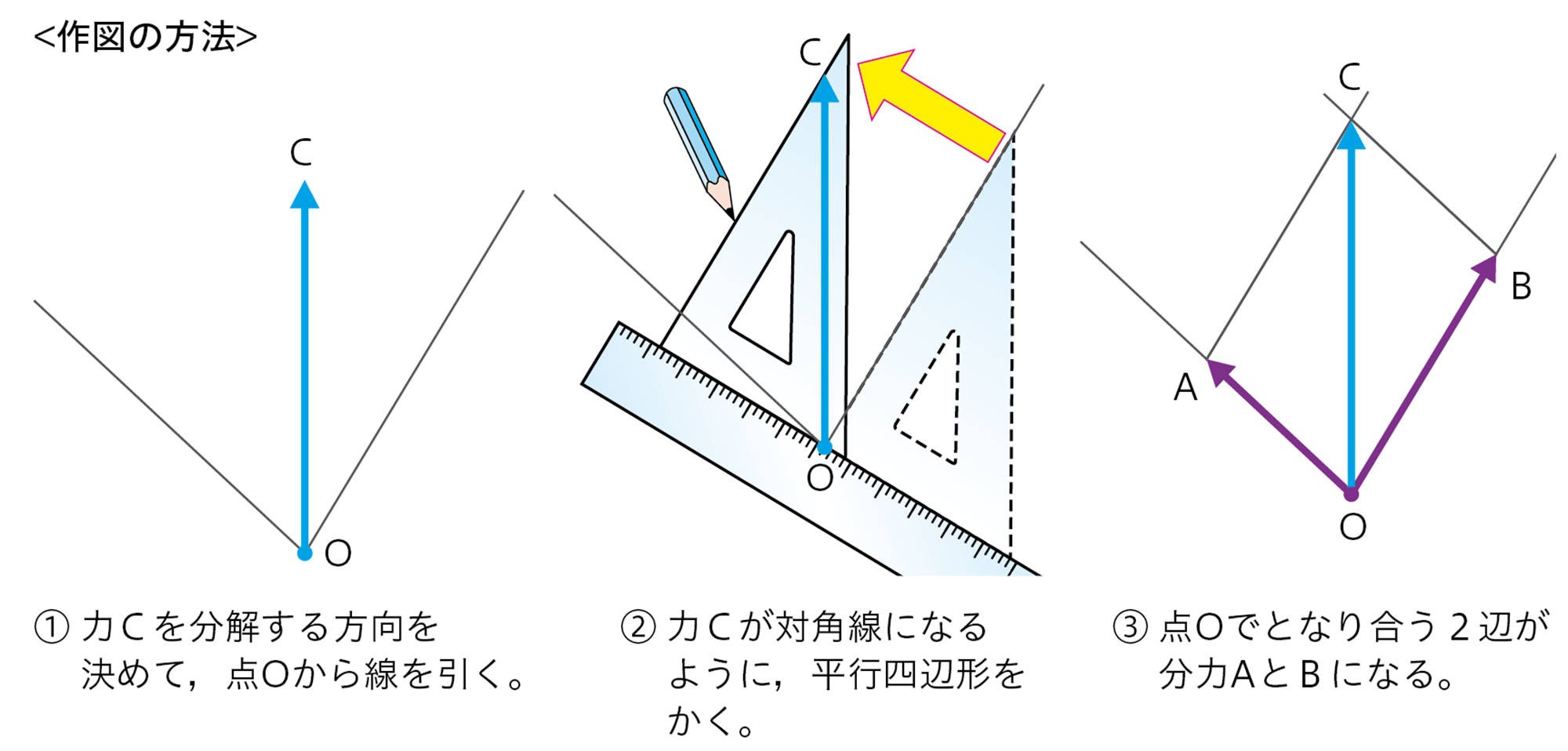
４ 力の分解
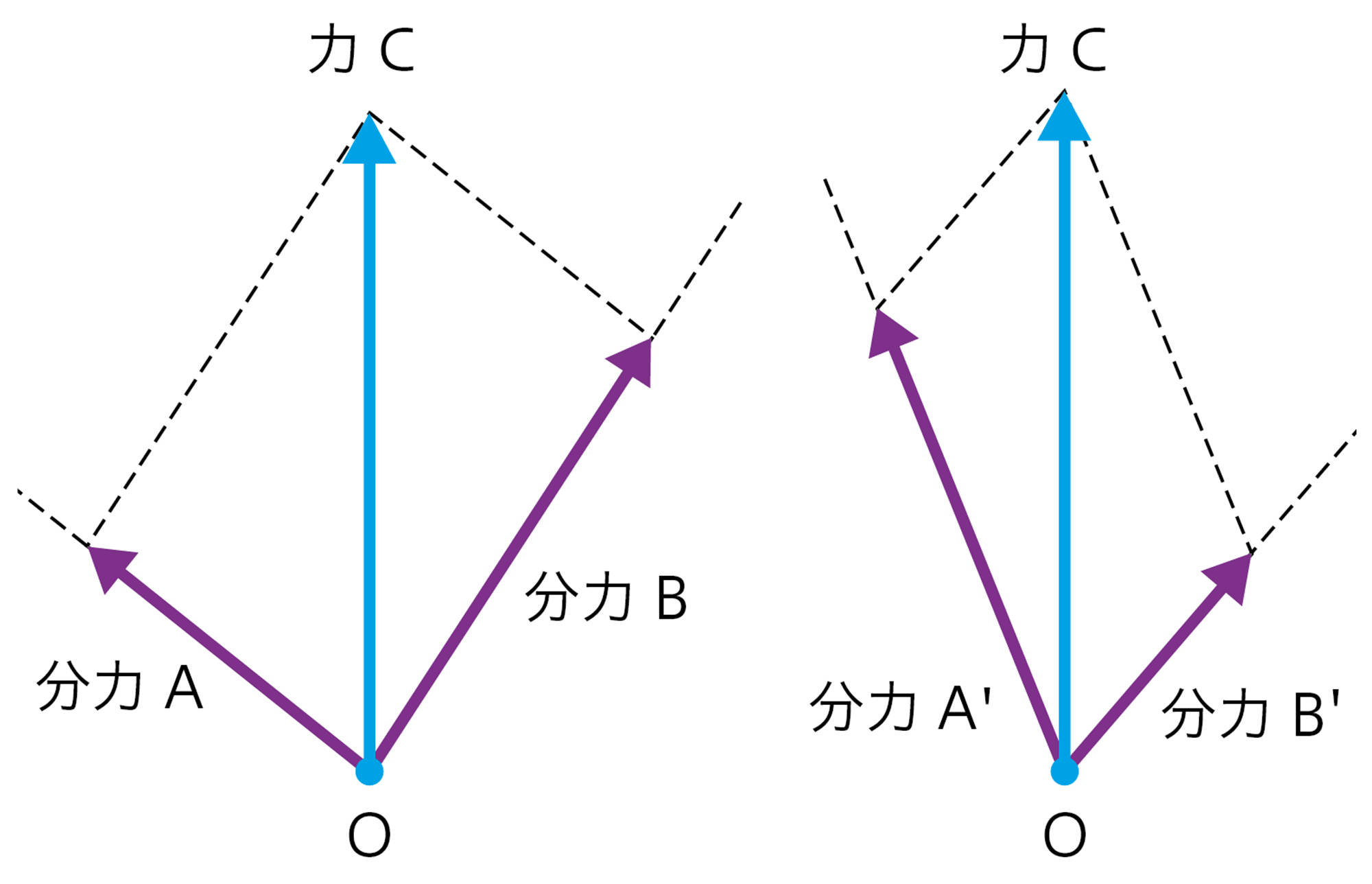
1つの物体が受ける2力は，合成して1つの合力におきかえることができた。反対に，1つの力からそれと同じはたらきをする2力に分けることもできる（図17）。これを力の分解といい，分けた2力をもとの力の分力という。
１つの力を分解するときは，分解する方向を何通りも考えることができます。そのため，分力は何通りも求められます。
力Cの矢印を対角線とする平行四辺形の2辺を求めればよい。
図17 力の分解
※このウェブページは中学校理科3年の学習内容です。<3年p.243>
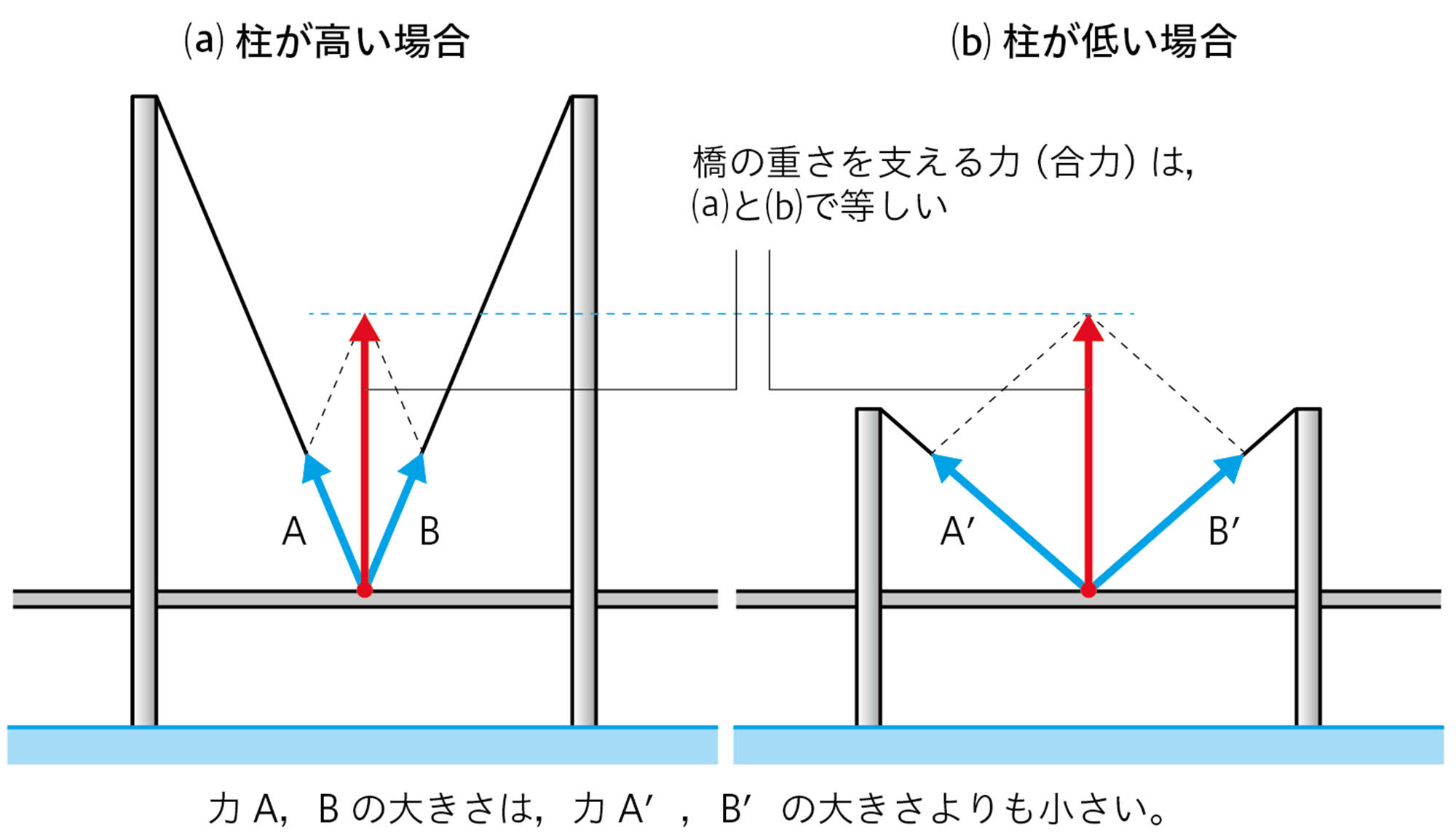
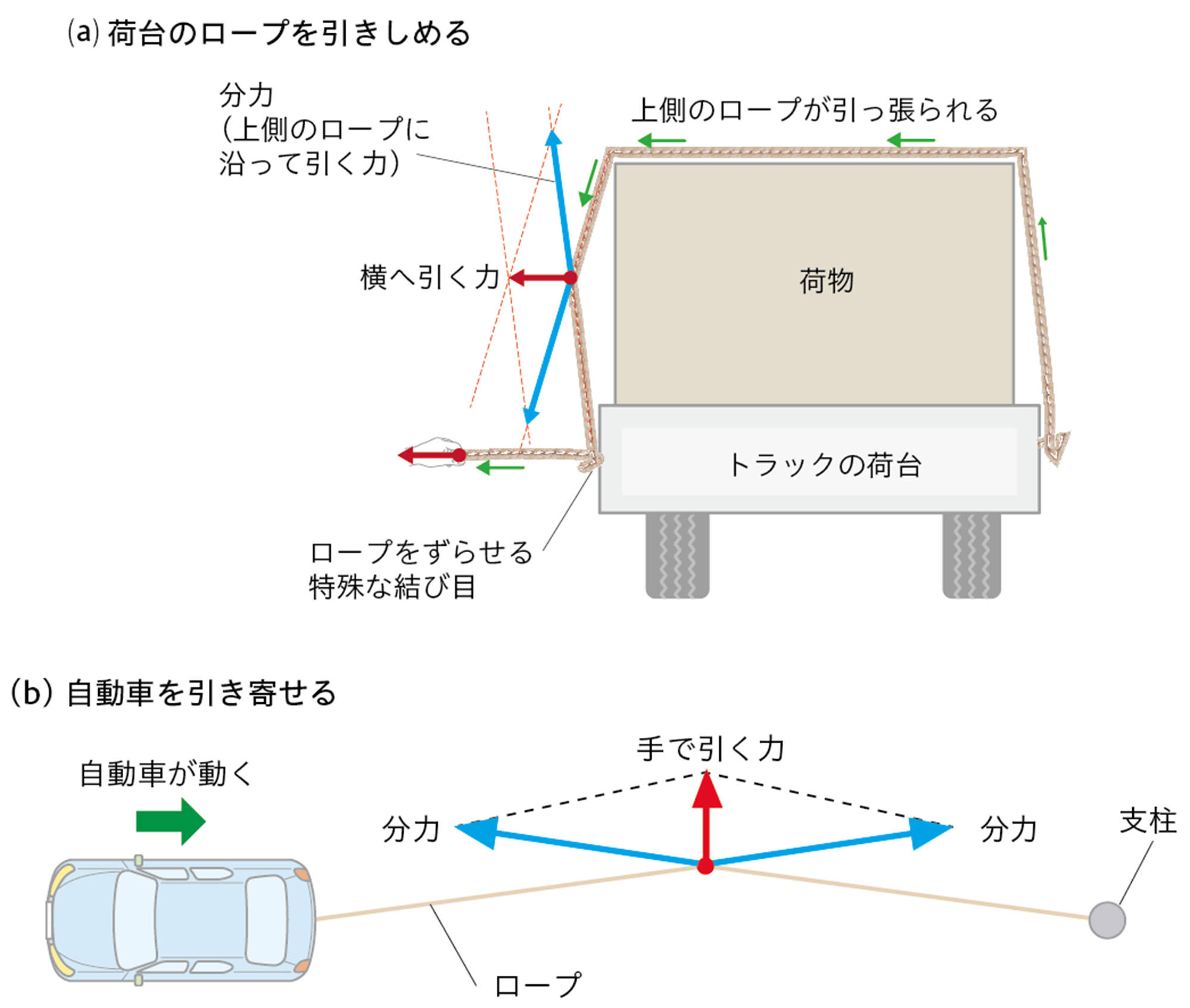
資料 力は分力の角度で強くなる
● 斜張橋──橋の重さをワイヤーで支える
図の斜張橋では，両側のワイヤーの力A，Ｂの合力が橋の重さを支えています。柱が高い⒜の方が，柱が低い⒝よりも，ワイヤーにかかる力を小さくすることができます。ただし，実際の設計では，材料費を少なくするなどの点も考慮して柱の高さが決められます。
● 刃で切り分ける
刃は，力がはたらく面積を小さくして圧力を高めるだけでなく，分力も応用しています。たとえば包丁で野菜などを切るとき，包丁が下向きに押す力が小さくても，野菜を左右に押し分ける力は大きくなります。
●ロープを力強くしめる
トラックに積んだ荷物にロープをかけて固定するとき，ピンと張ったロープを横に引いてパンッパンッとはじくことがあります。このとき，図⒜のように，ピンと張ったロープを横に引くと，引いたところを作用点としてロープに沿った方向の大きな分力が生じ，ロープをさらに引きしめる力となるからです。ロープが引きしめられたら，ロープと荷物のすき間がもとにもどるまでの一瞬に，特殊な結び目を通してロープを引き寄せて，ロープがゆるまないようにします。
このようなロープのはたらかせ方を利用すると，図⒝のように，人の手で自動車を引き寄せることもできます。
