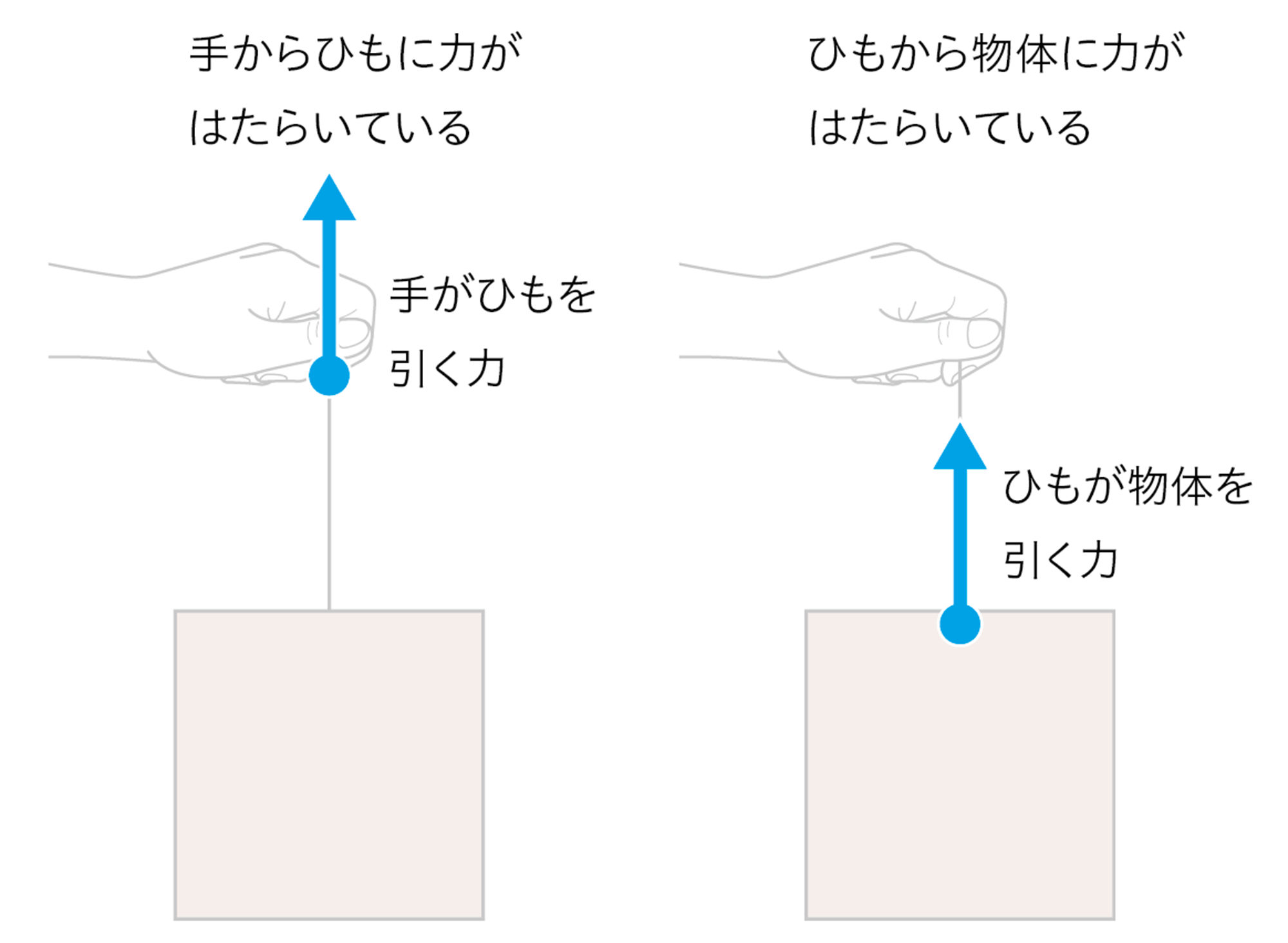
※このウェブページは中学校理科１年の学習内容です。<1年p.130>
１｜力の表し方
１ 力による現象
力は目に見えないが，私たちは，決まった現象を見たときに「力がはたらいている」と表現する。「力がはたらいているとき」は科学的にどのように説明できるだろうか。
探究６ 「力がはたらいている」とはどのようなときか
準備
物体（ボール，木の直方体など）
① 物体に力を加え，物体のようすがどのように変化するかを観察する。
② 力がはたらいている場面のさまざまな例を整理する。
物体に力を加えたときのようすや，そのほかの場面を観察した結果を記録する。
③ 力がはたらいている場面を見つけるには，どのような共通点に注目すればよいか考察する。
※このウェブページは中学校理科１年の学習内容です。<1年p.131>
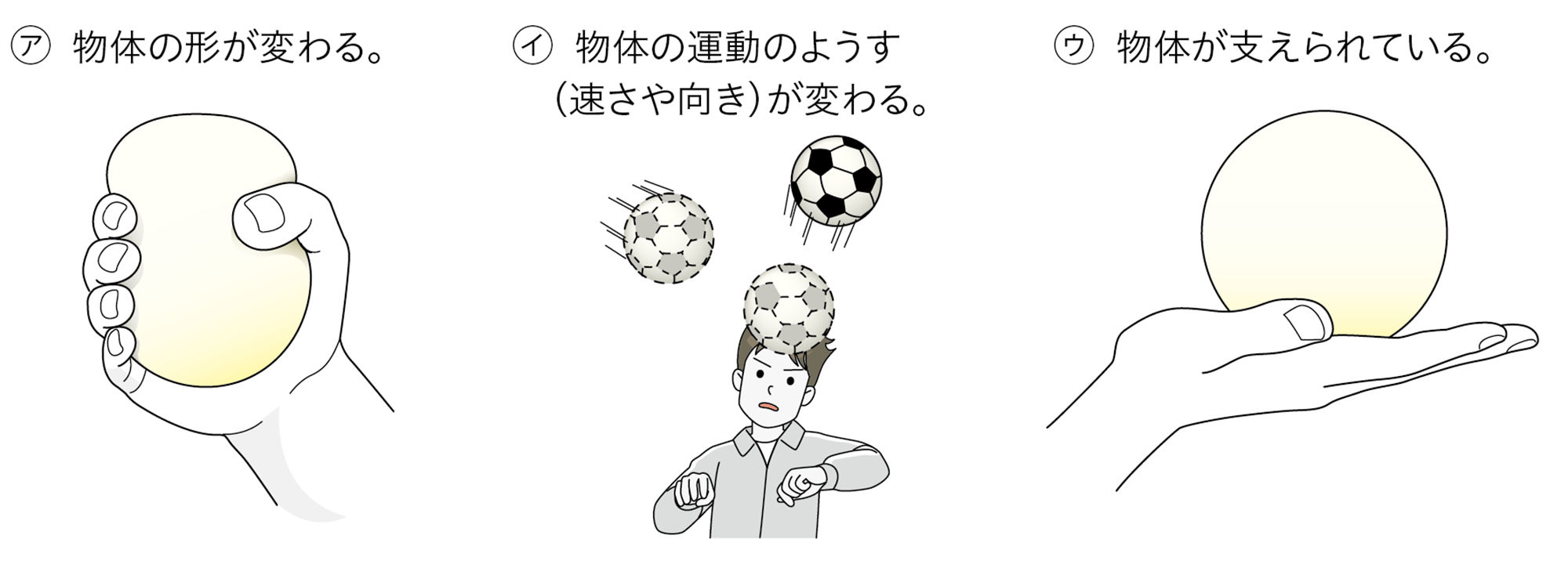
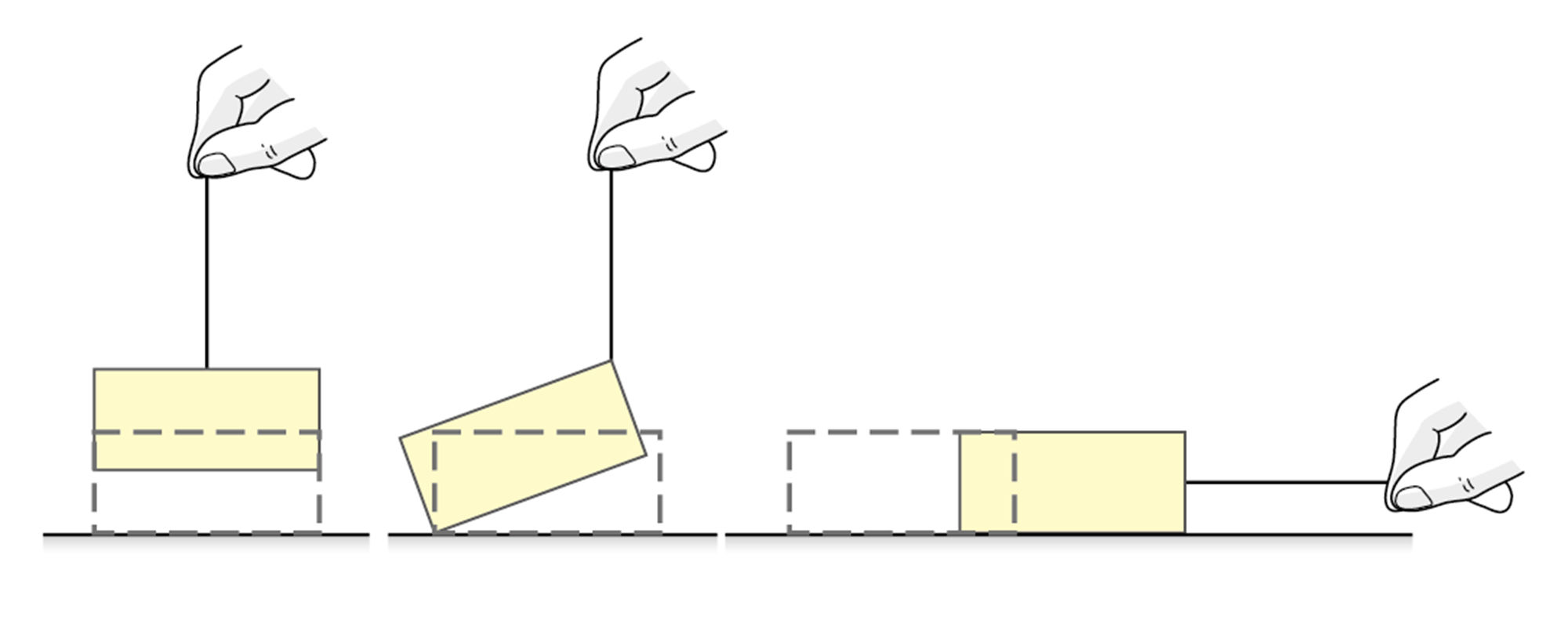
前ページの「探究6」を行うと，身のまわりの力がはたらいている場面は図2の㋐〜㋒の3つにまとめられることがわかる。つまり，㋐〜㋒に1つでも当てはまる物体には，「力がはたらいている」と考えることができる。
図2から，力のはたらきとして，
㋐ 物体の形を変える
㋑ 物体の運動のようすを変える
㋒ 物体を支える
という言い方もできますね。
２ 重力
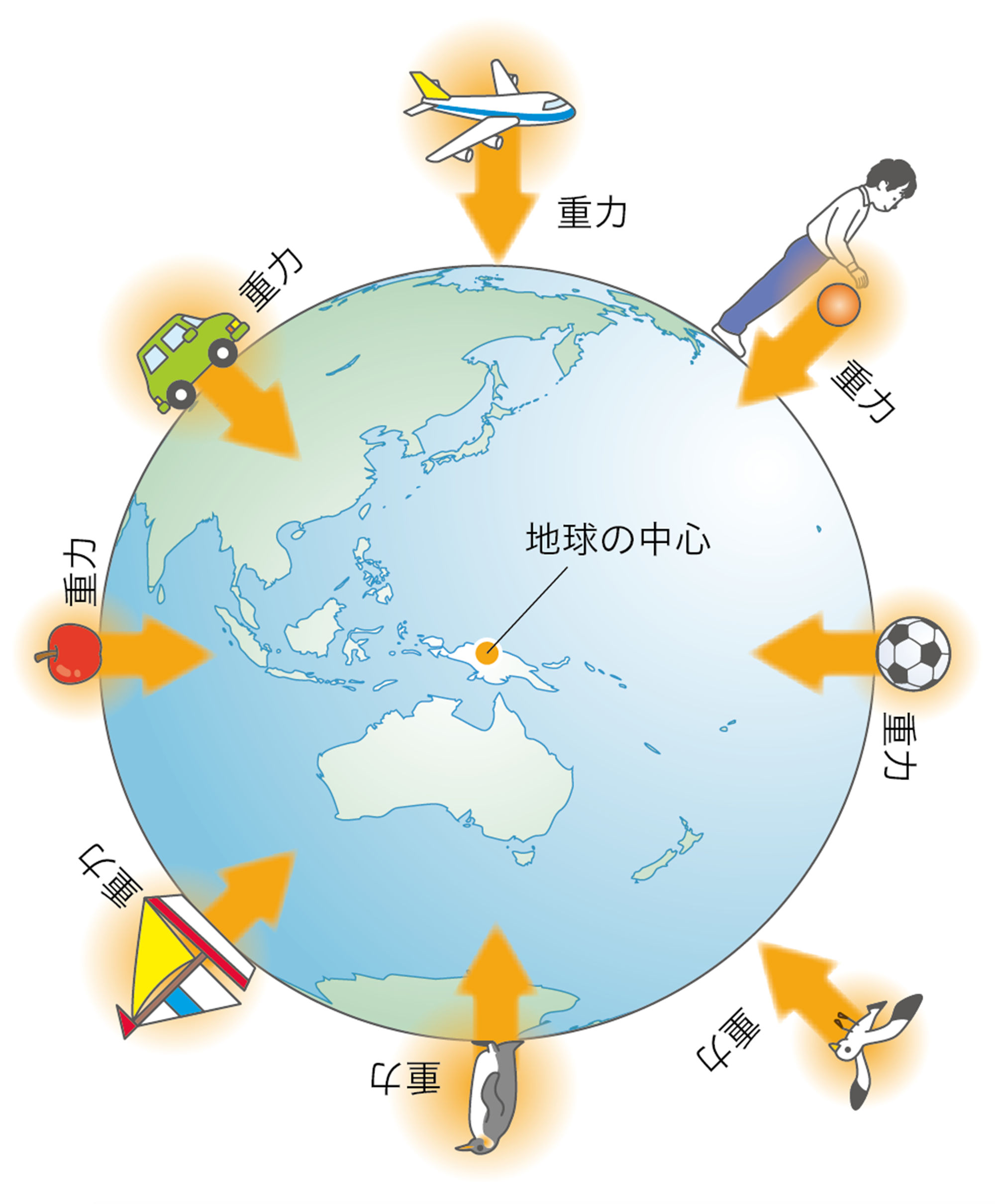
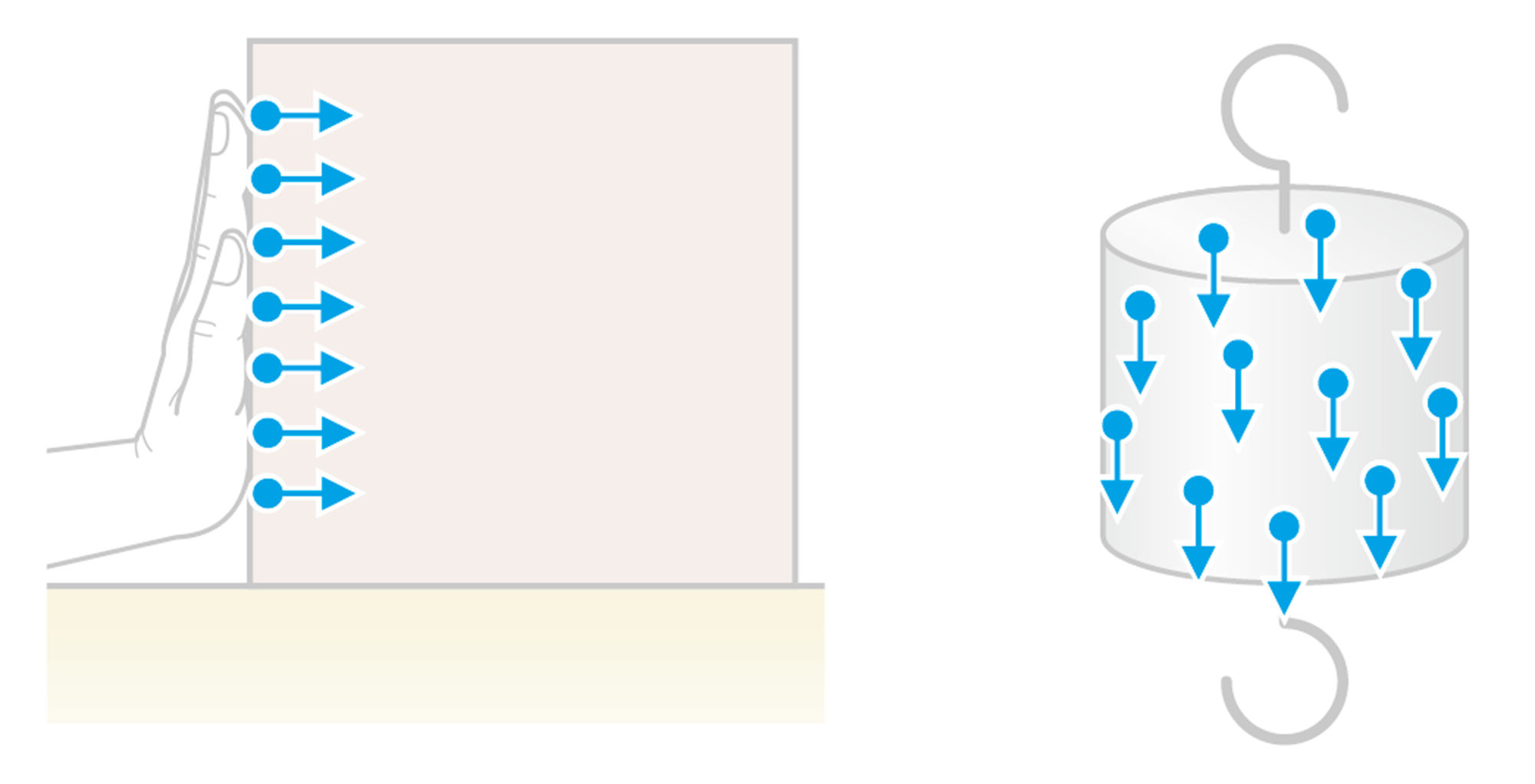
図2㋒のとき，物体から手をはなすと，物体は地面に落ちる。物体を上に向かって投げても，やがて落ちてくる。このように運動のようすが変わることから，物体には，常に何かの力がはたらいていることがわかる。
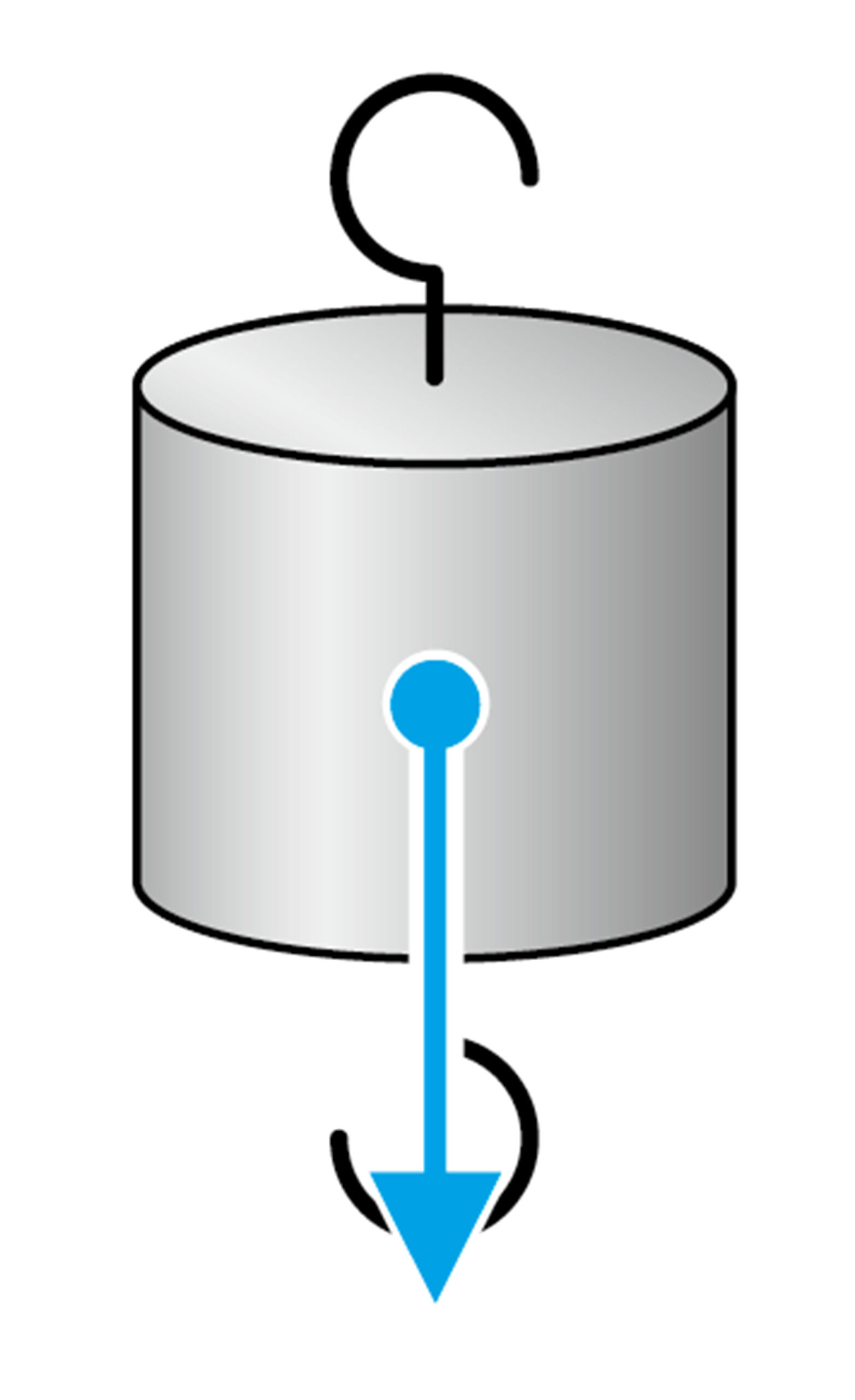
地球上のすべての物体には，地球がその中心へ向かって引きつける力がはたらいている（図3）。この力を重力という。物体の重さとは，物体にはたらく【重力】の大きさのことである❶。
地球上のすべての物体は，重力によって地球の中心に向かって引きつけられている。この中心の方向を，その場での「鉛直方向」という。空を飛ぶ飛行機や鳥にも，鉛直方向の重力がはたらいている。
図3 重力
私たちが日常で使う「重い」は，「物体にはたらいている重力が大きい」状態である。逆に「軽い」は「はたらいている重力が小さい」状態といいかえることができる。
図4 重い・軽い厳密には，同じ物体であっても地球上の場所によって，重力の大きさはごくわずかに異なります。しかし，その差は非常に小さいため，地球のどこでも「重力はほぼ等しい」と考えます。
❶ これから「重さ」を， 「質量（gの単位で表す）」とは区別して考えていく。
※このウェブページは中学校理科１年の学習内容です。<1年p.132>
３ 重力と力の大きさの表し方
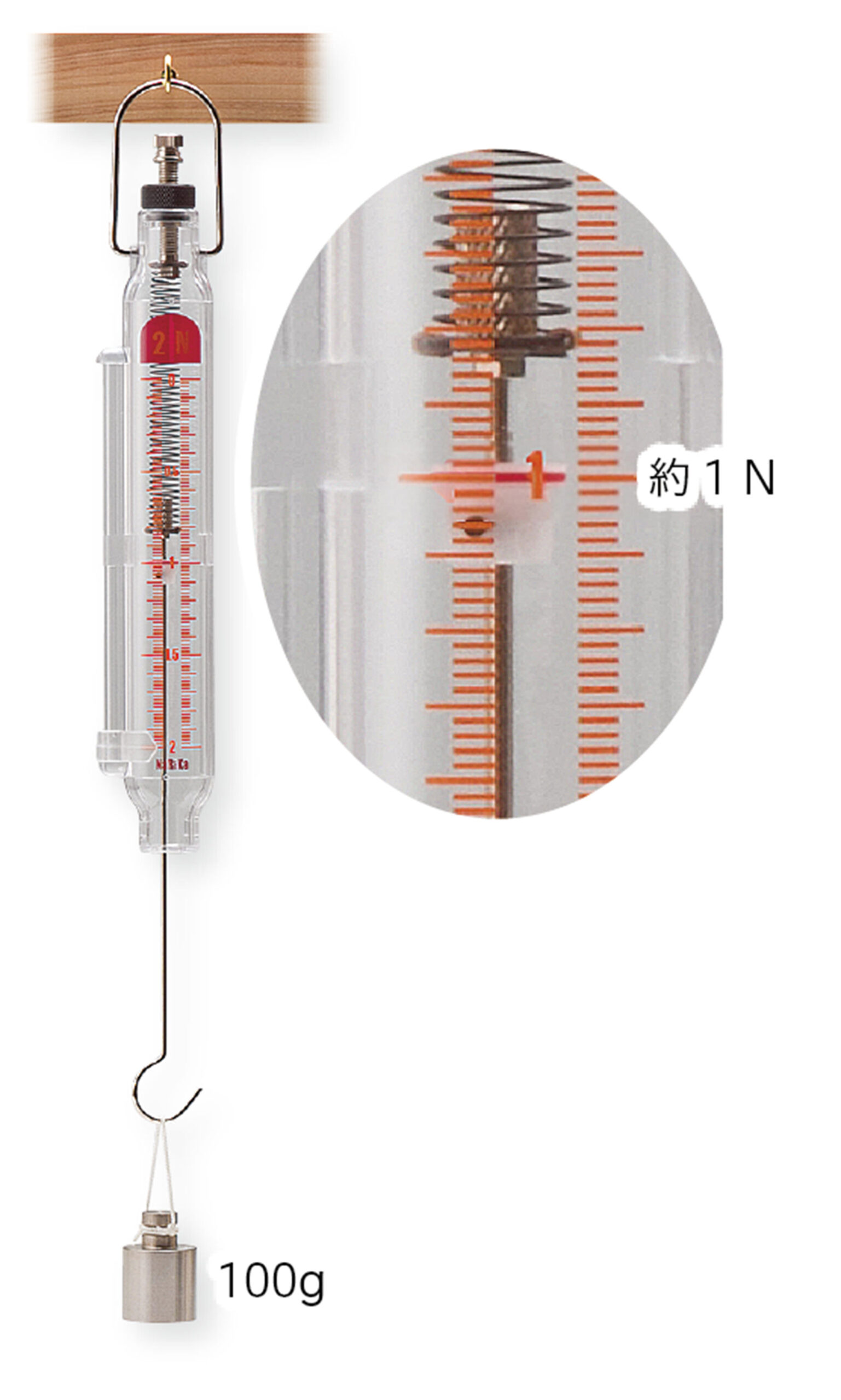
重力の大きさは，【ニュートン】❶（記号N）という単位を使って表し，ニュートン目盛りのばねばかりを使ってはかることができる（図5）。質量100g の物体をばねばかりにつるすと約1Nを示す。つまり，100g の物体にはたらく重力（重さ）は約1Nである。
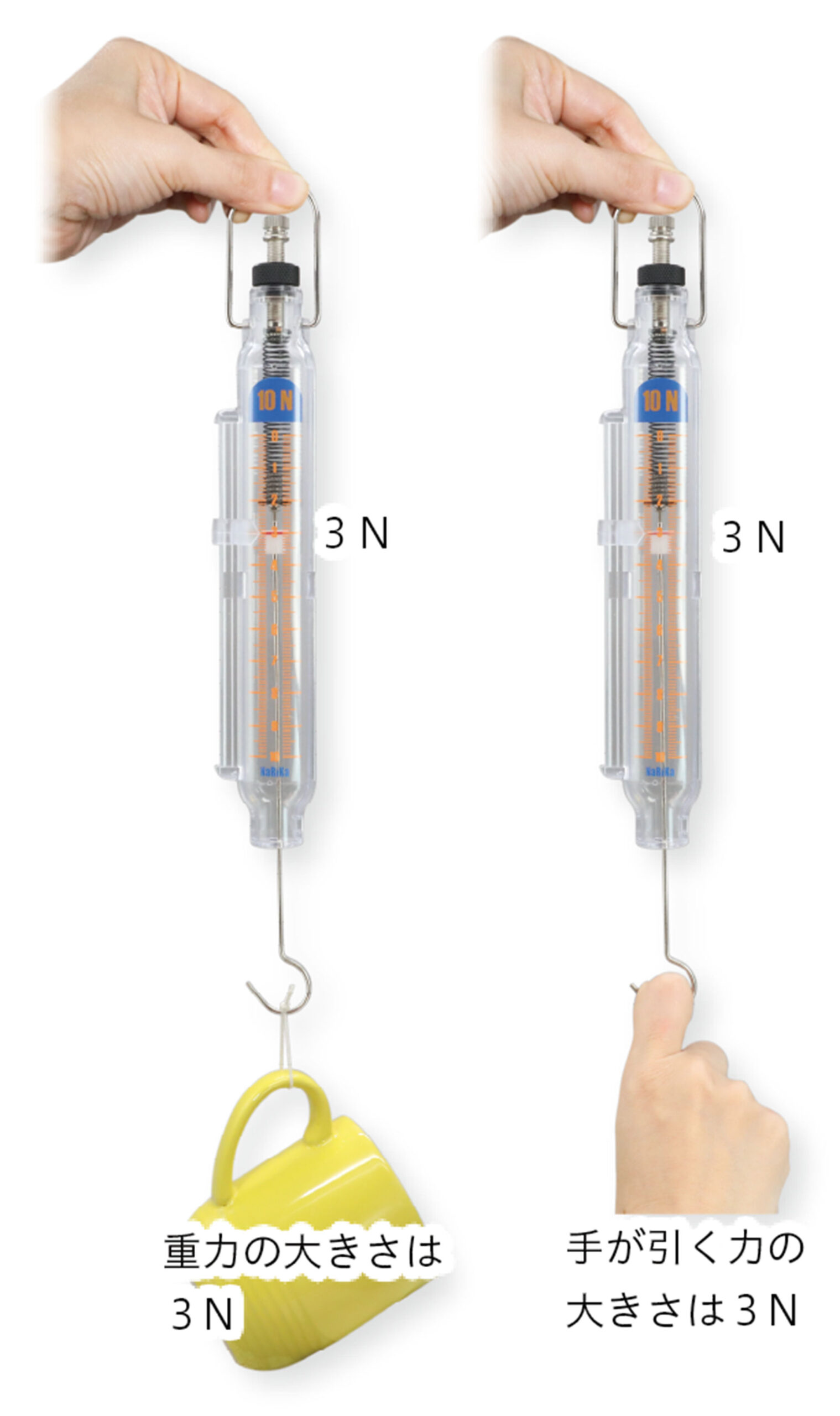
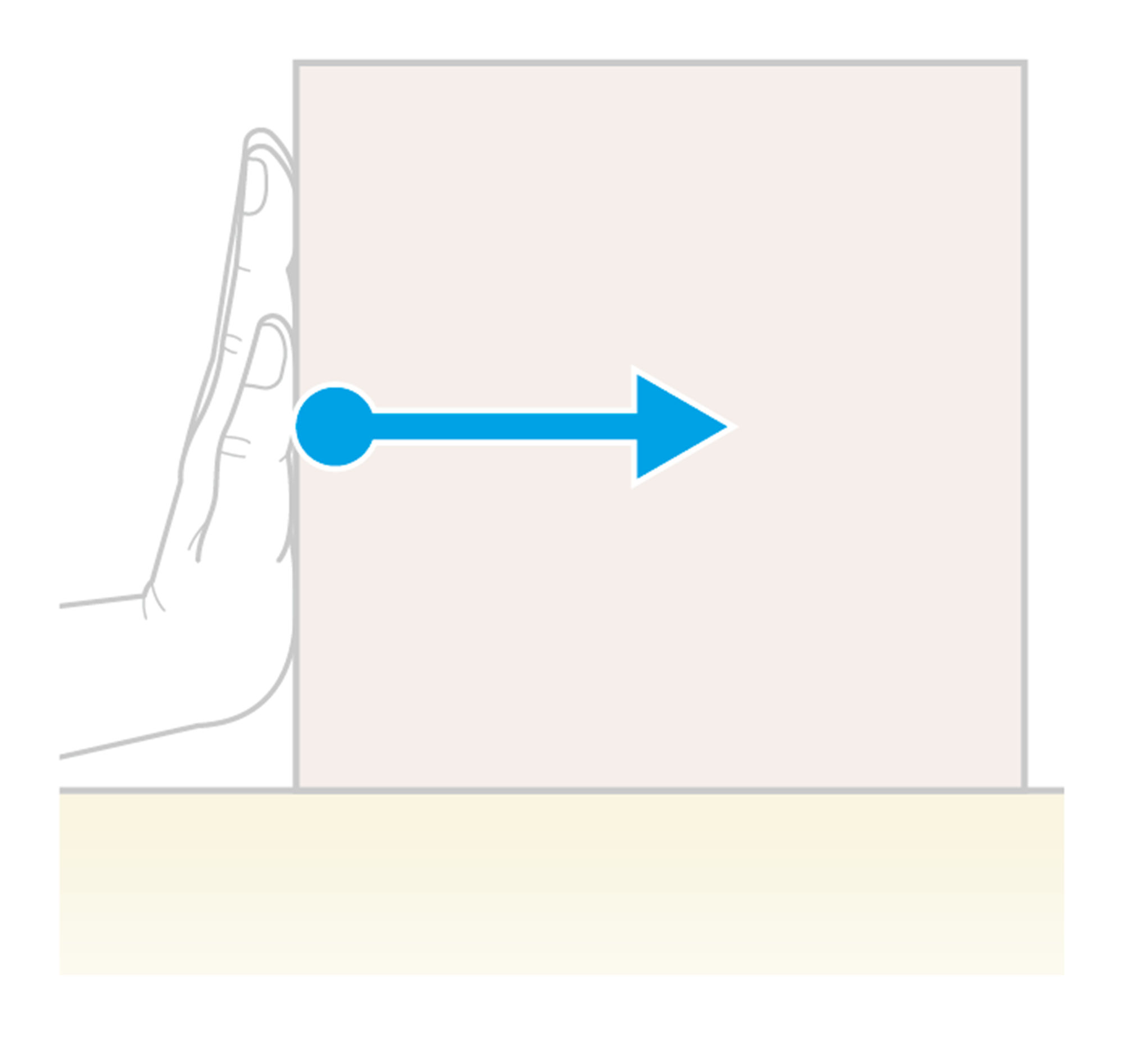
重力以外のどのような力でも，このはかりを用いることで，その力の大きさをはかることができる（図6）。
100gの物体にはたらく重力は約1N（正確には約0.98N）であり，200gの物体の場合は約2N，300gの物体の場合は約3Nである。
図5 重力の大きさ
コップをつり下げても手で引いても，目盛りが同じ３Nを示しているのであれば，はかりにはたらく力は同じである。
図6 重力の大きさと力の大きさばねばかりは，水平にしても使うことができます。
押し棒を使って，押す力をはかることもできます。
食品の量り売りなどで使われる「台ばかり」は，ばねばかりの一種である。のせた物体が台を押す力の大きさにしたがって針が動く。この力は，物体にはたらく重力（重さ）と大きさが等しいので，本来，台ばかりは重力の大きさをはかるものである。しかし，ニュートン（N）のかわりにグラム（g）の単位で目盛りがつけられ，１Nの力のとき針が目盛りの100gをさすようにつくられているため，だいたいの質量をはかる道具として日常生活で使われている。ただし，精密に質量をはかるときは，上皿てんびんや電子てんびんを使う。
図7 台ばかり
❶ 重力を発見したイギリスの科学者アイザック・ニュートン（1643〜1727年）の名前にちなんでいる。
※このウェブページは中学校理科１年の学習内容です。<1年p.133>
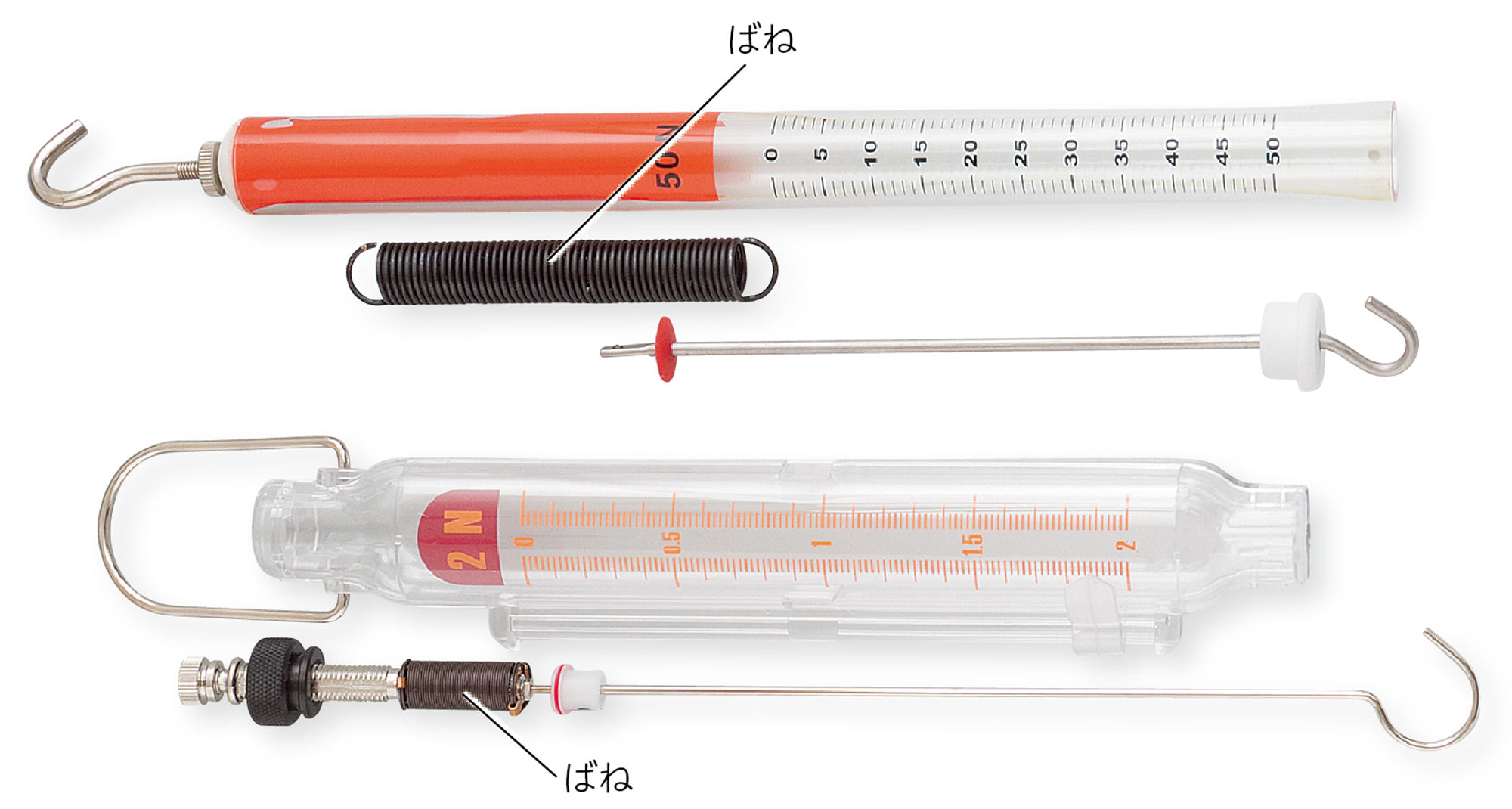
４ ばねの性質と力
ニュートン目盛りのばかりにはいくつも種類があり，はかる物体の重さにより，はかりを変える必要がある。ばねばかりのしくみについて，どのように科学的に探究できるだろうか。
探究７ ばねの伸びと力の関係
ばねばかりは，力がはたらいたときのばねの伸びで力の大きさをはかっています。ばねにはたらく力とばねの伸びの関係について調べてみましょう。
50N用のばねは太いね。ばねにもいろいろな種類があるね。
ばねにつるすおもりの重さと，ばねの伸びの間には，どのような関係があるか。
おもりが増えるほどばねが伸びるから「はかり」として使えるんだね。
たとえば100gのおもりをつるしたとき，ばねは決まった長さだけ伸びるはず。
何を変えると，ばねの伸びが変わるのか，関係を予想してみよう。
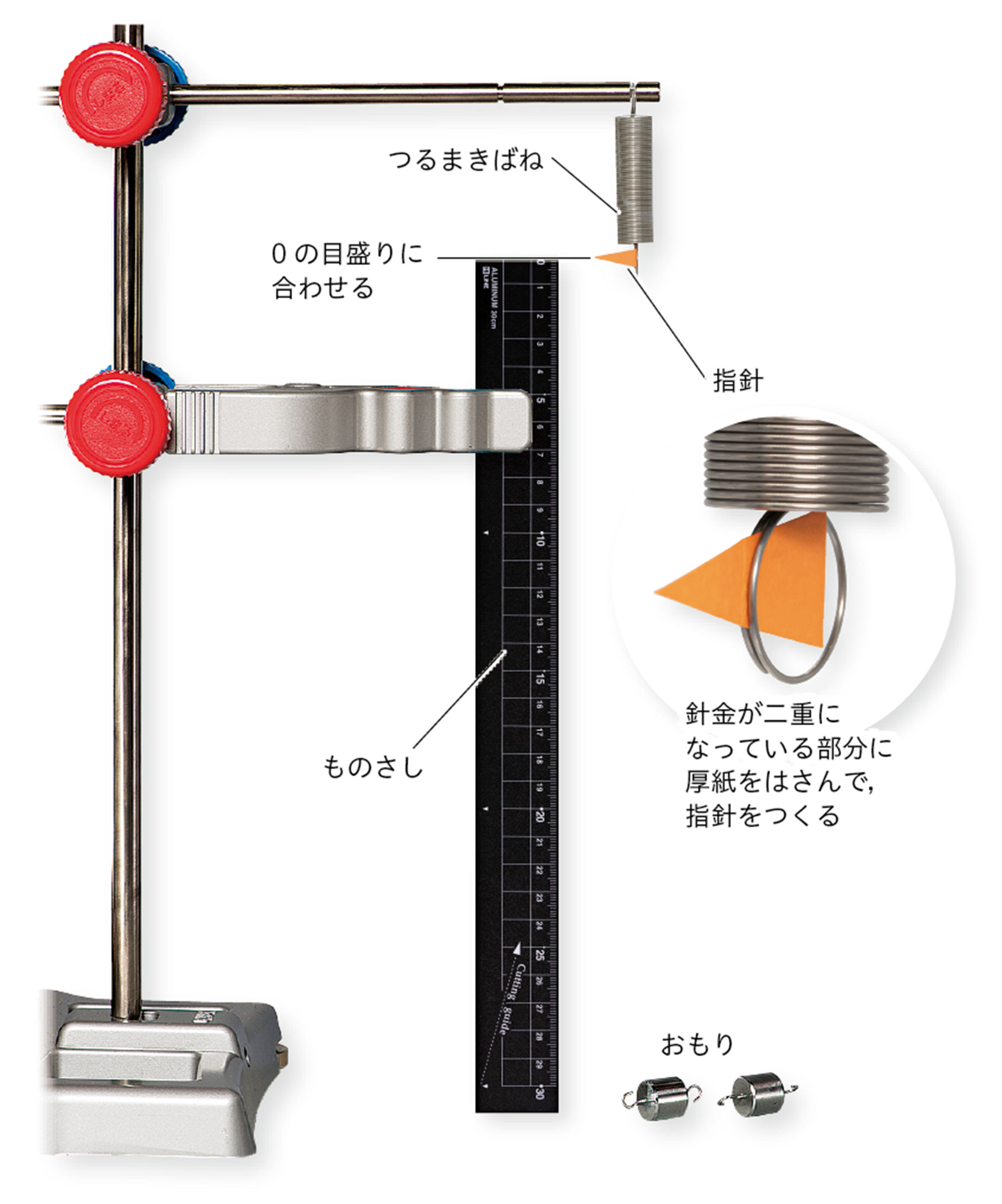
ばねにつるすおもりをだんだん増やして，ばねの伸びをはかっていこう。
必要な道具は，ばね，おもり，あとは何だろう。
１個10gのおもりを使うことができれば，おもり1個を下げるたびに，約0.1Nの力が加わると考えられるよ。
※このウェブページは中学校理科１年の学習内容です。<1年p.134>
準備
つるまきばね（２種類），おもり（同じ質量のものを数個），スタンド，ものさし，厚紙
１．実験装置を組み立てる
図のように，三角に切った厚紙をばねにはりつけて指針（目盛りをさす印）とする。
ばねにおもりをつるさない状態で，指針がものさしの0の目盛りに合うように装置を組み立てる。
２種類のばねの一方をA，もう一方をBとします。両方のばねを順に使って実験してみましょう。
ばねを２種類使うのはなぜだろう？どんなばねでも，同じような決まりがあるかを調べるためかな？
そうですね。１つのばねを調べただけだと，そのばねだけの性質かもしれません。調べる例を地道に増やしていくことも，自然の決まりを見つけていくための大事な活動です。
２．おもりをつるしてばねの伸びを測定する
ばねにつるすおもりを1個，2個…と増やしていき，それぞれのばねの伸びを測定する。
注意 加える力が大きすぎると，ばねが伸びきってこわれてしまうので注意する。
※このウェブページは中学校理科１年の学習内容です。<1年p.135>
ポイント
結果を表に記入する。100gのおもりにはたらく力（重力）の大きさを1Nとする。
ポイント
補充資料p.214の「グラフのかき方」にしたがって結果をグラフに表す。グラフから，力の大きさとばねの伸びとの間にどのような関係があるといえるか。
※このウェブページは中学校理科１年の学習内容です。<1年p.214>
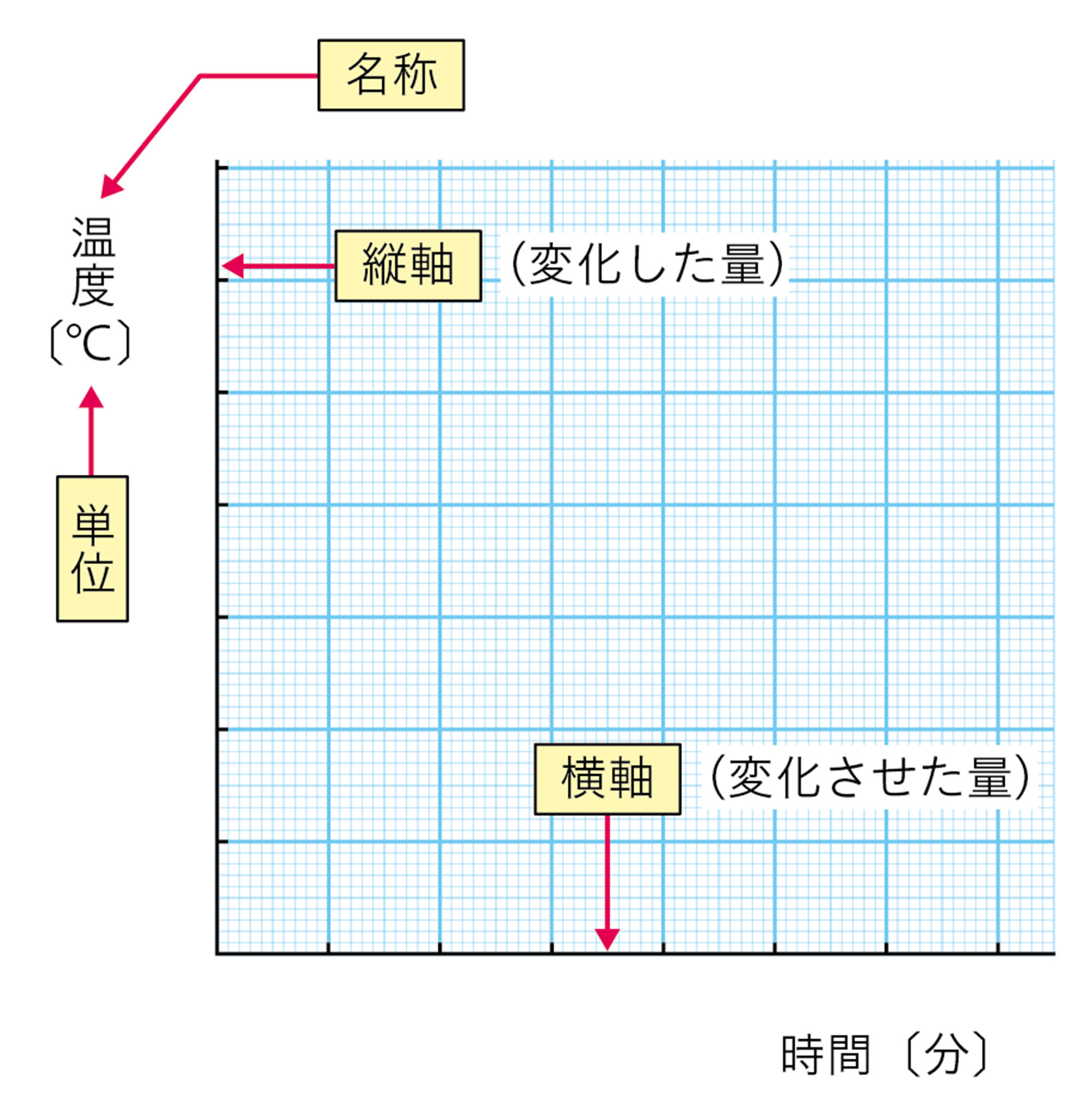
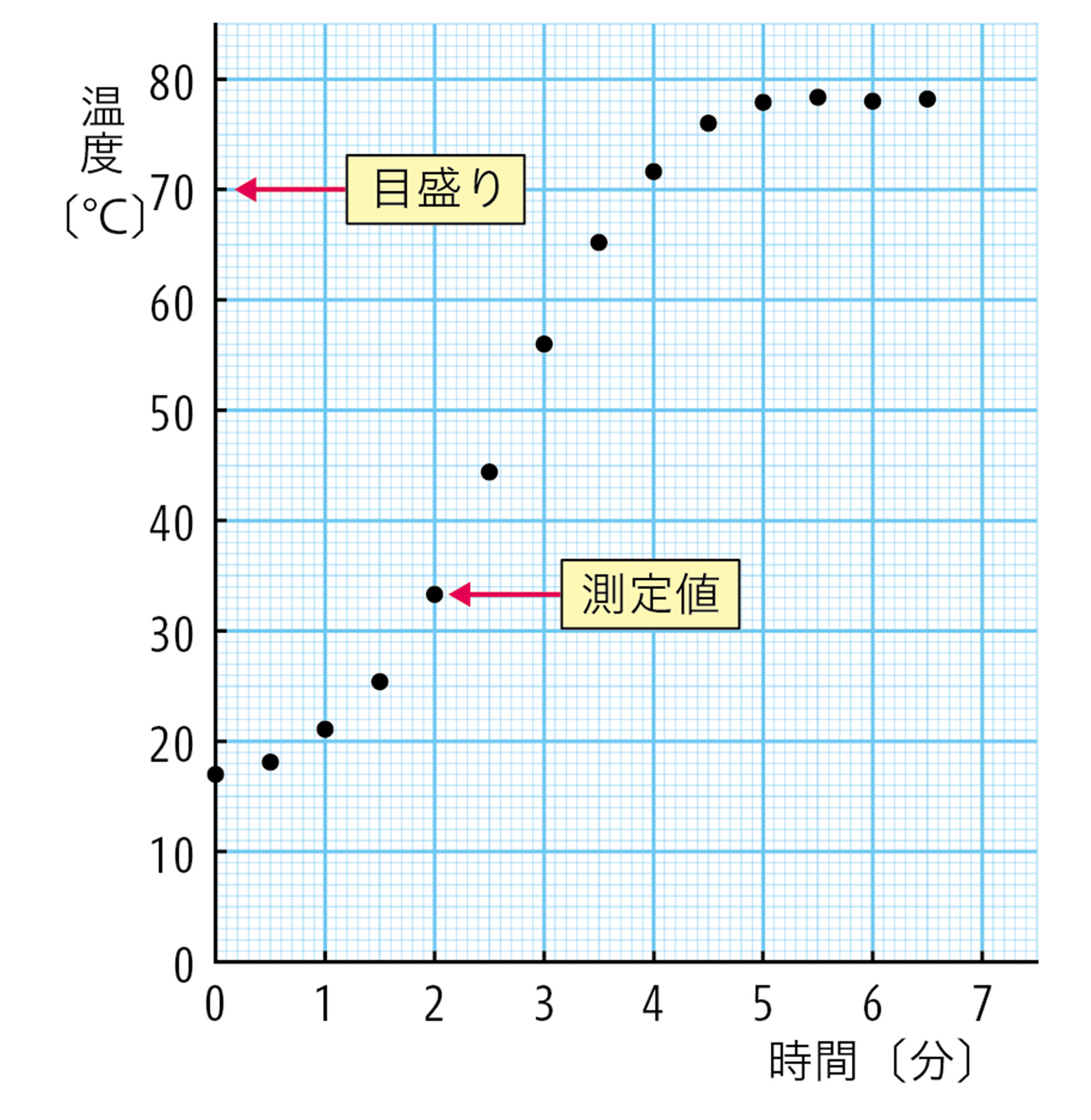
基本操作 グラフのかき方
① 横軸と縦軸にとる量を決める
・横軸には変化させた量（時間など）をとります。
・縦軸には変化した量（温度など）をとります。
・単位もかきます。
・測定値がすべてグラフにおさまるように，一目盛りの大きさを考えて目盛りをつけます。
② 測定値をはっきり記入する
●や○，×などの印で，はっきり記入します。
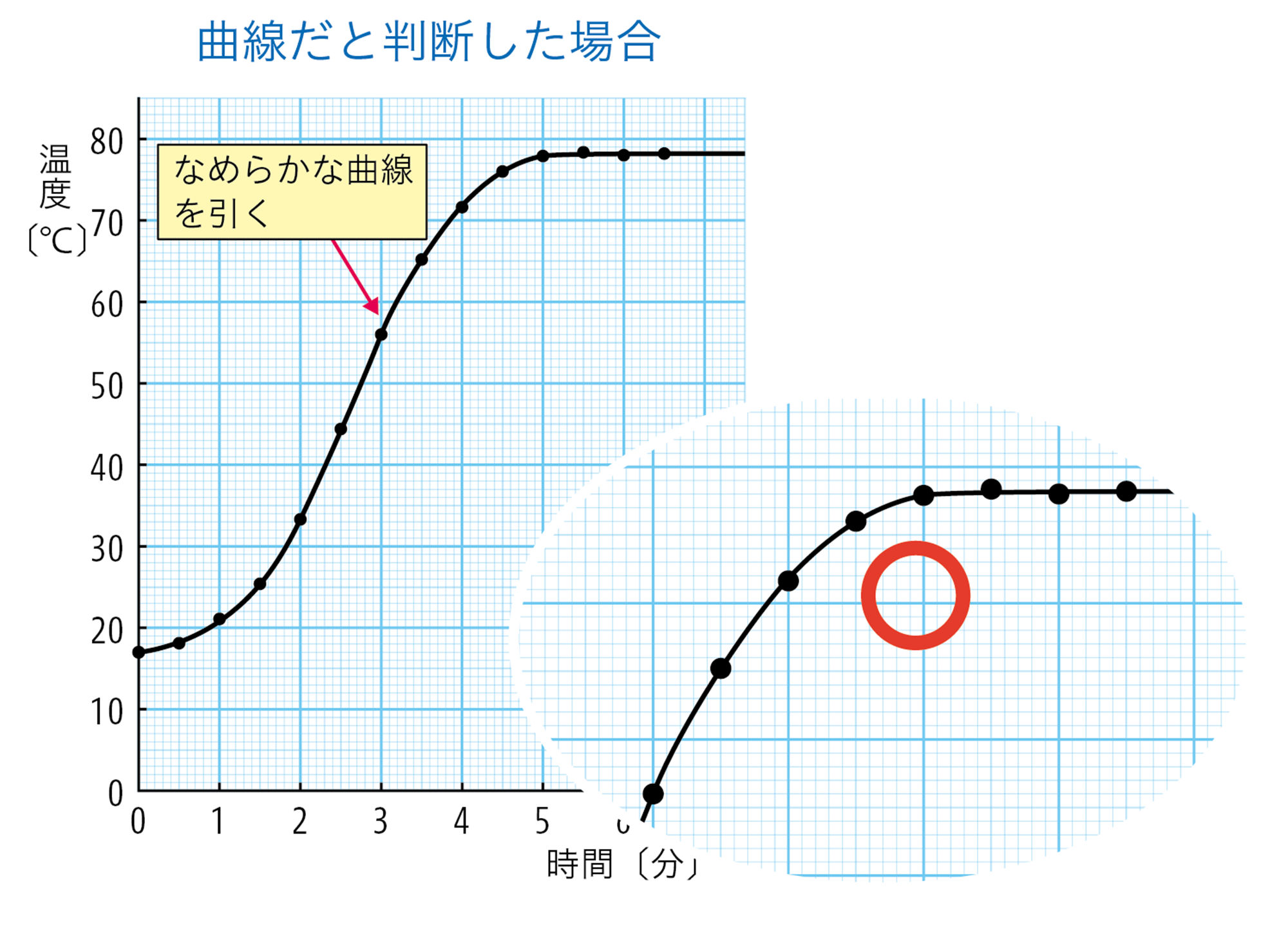
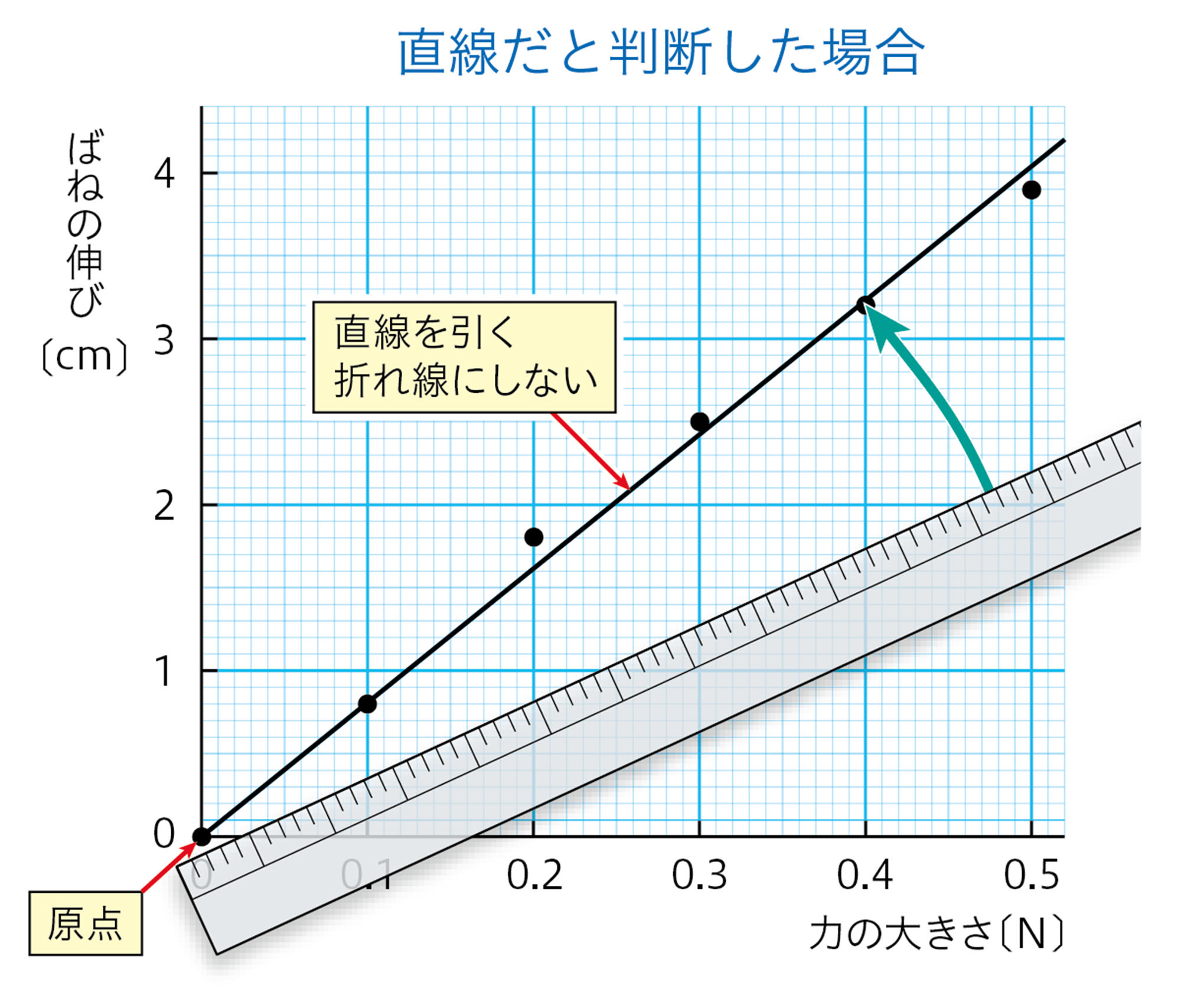
③ グラフが曲線か直線かを決める
測定値が曲線の上下に均等にちらばるように，曲線をえがきます。
測定値が線の上下に均等にちらばるように定規を当てて，直線を引きます。原点と最後の点を単に結ばないように気をつけましょう。
測定値を折れ線でつなぎません。これは測定値の誤差を考えてのことであり，また，自然現象はなめらかに変化する場合が多いため，それも意識しています。
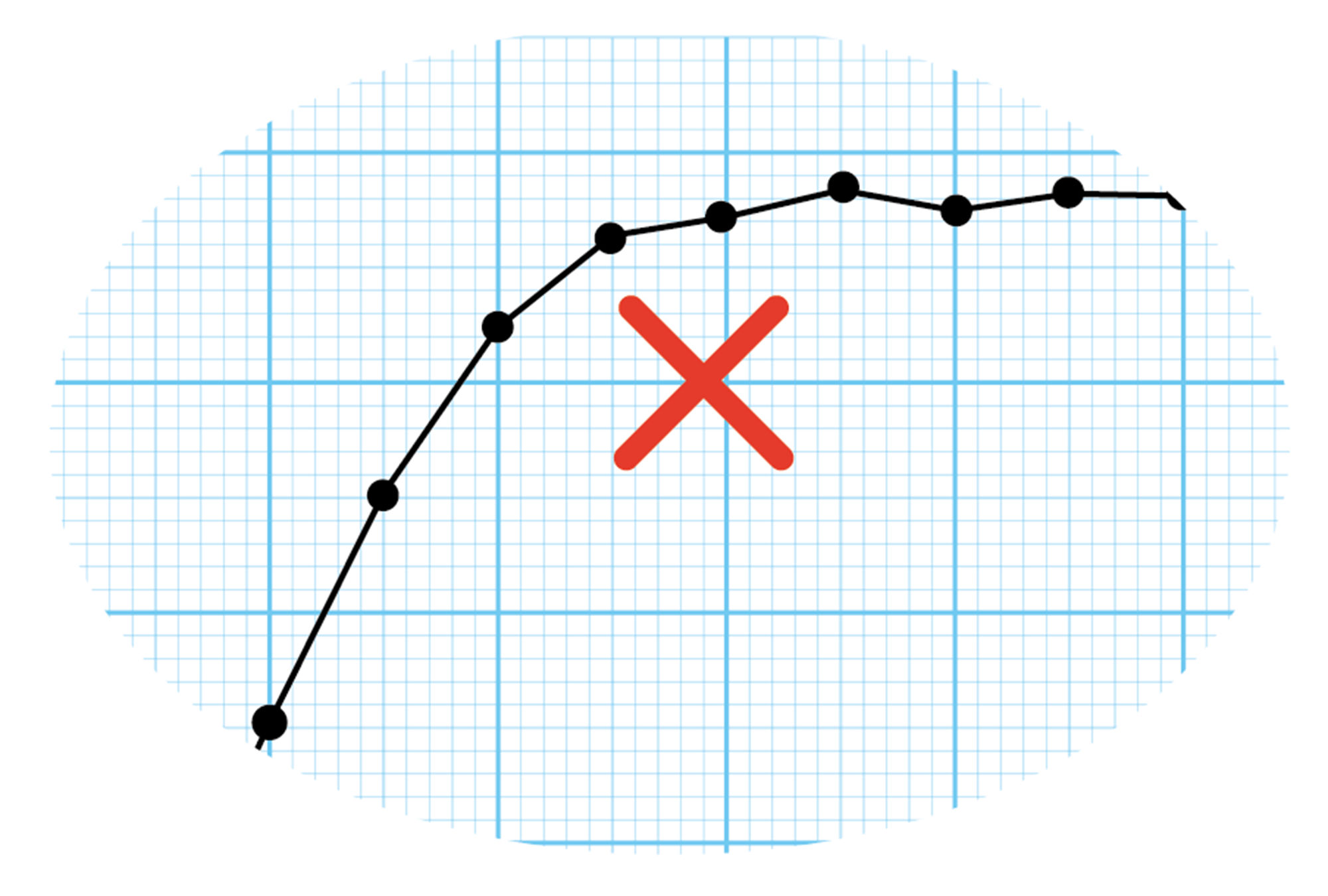
測定値をどのような線で結ぶと適切かは，本来は数学的な手法によって決めることができます。ただし，中学校で学ぶ範囲では，見た目で大まかに判断しています。
※このウェブページは中学校理科１年の学習内容です。<1年p.136>
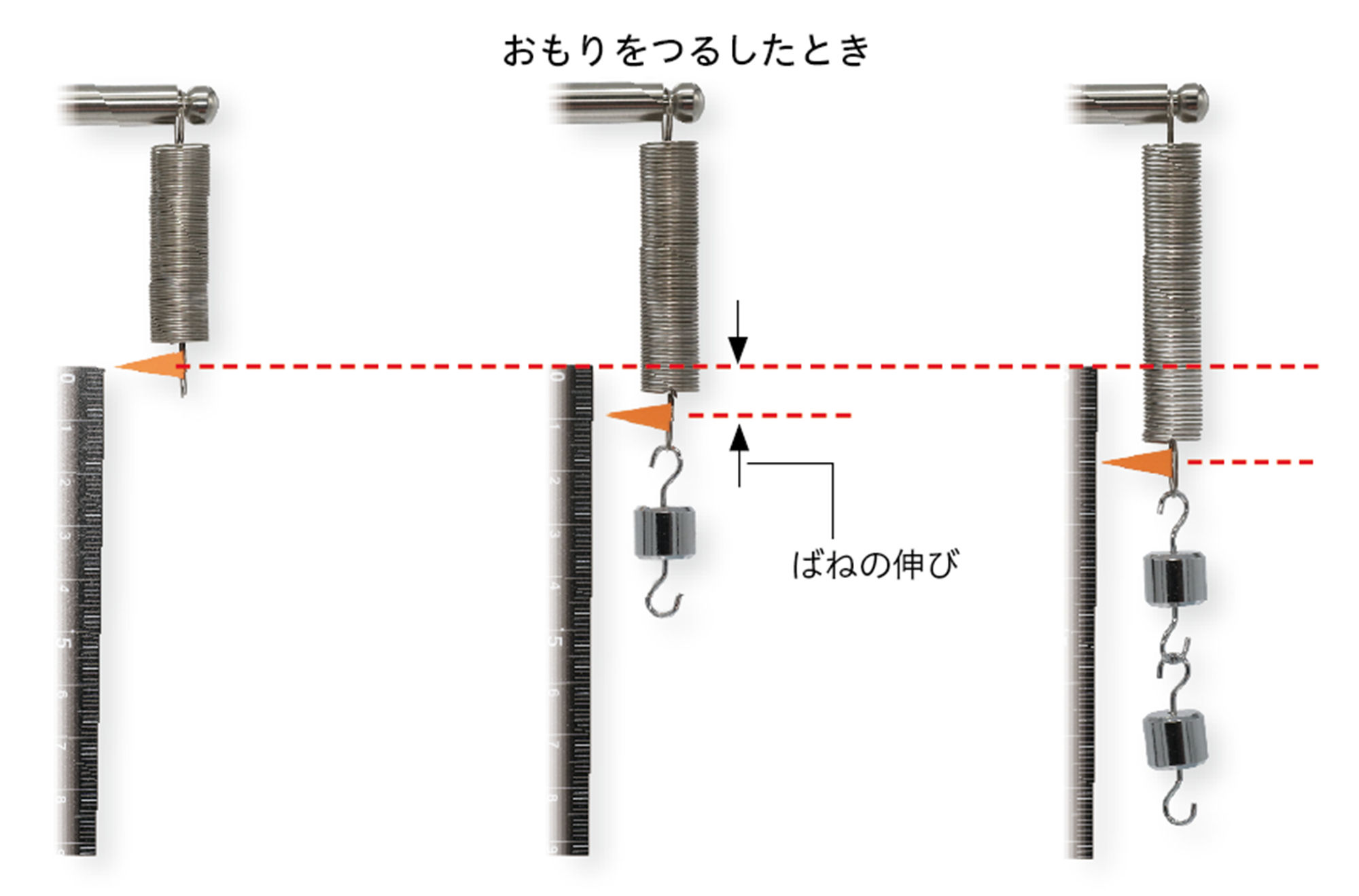
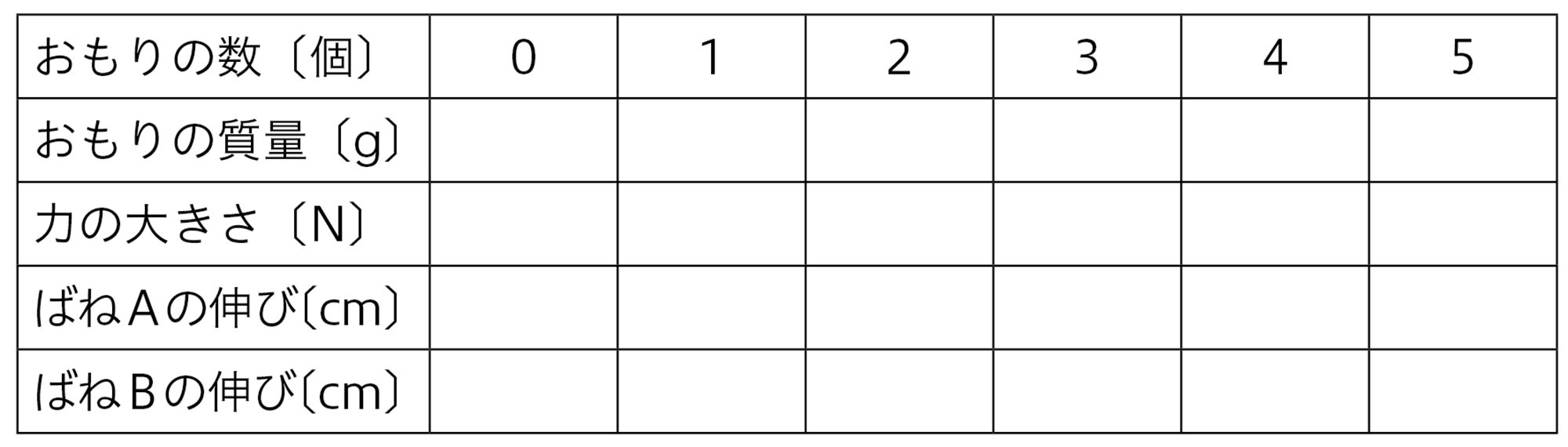
探究７ 結果から考察する
おもりの数が0のとき，伸びは０である。これも測定値と考える。
表1 探究7の結果例
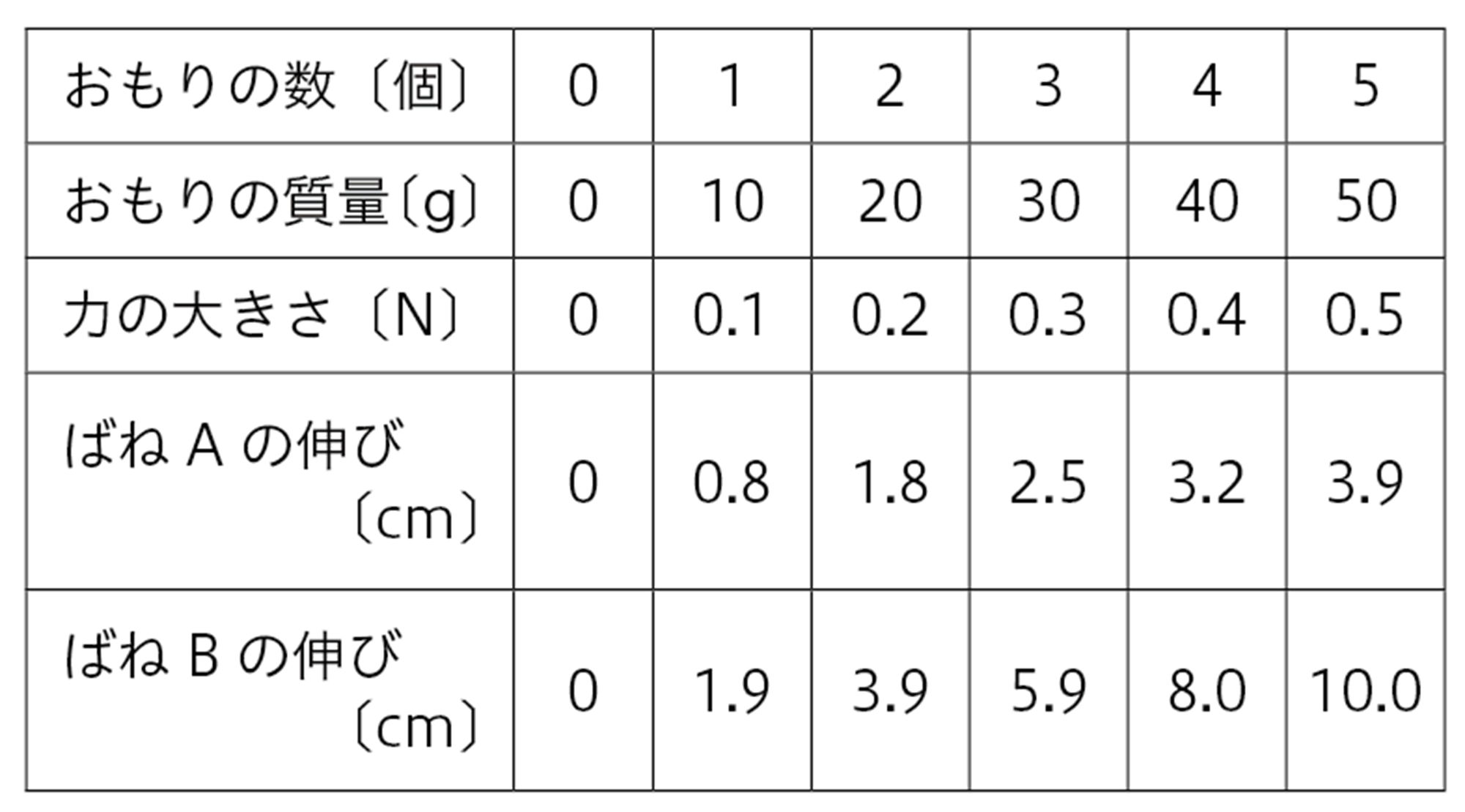
実験の結果をまとめると表1のようになった。
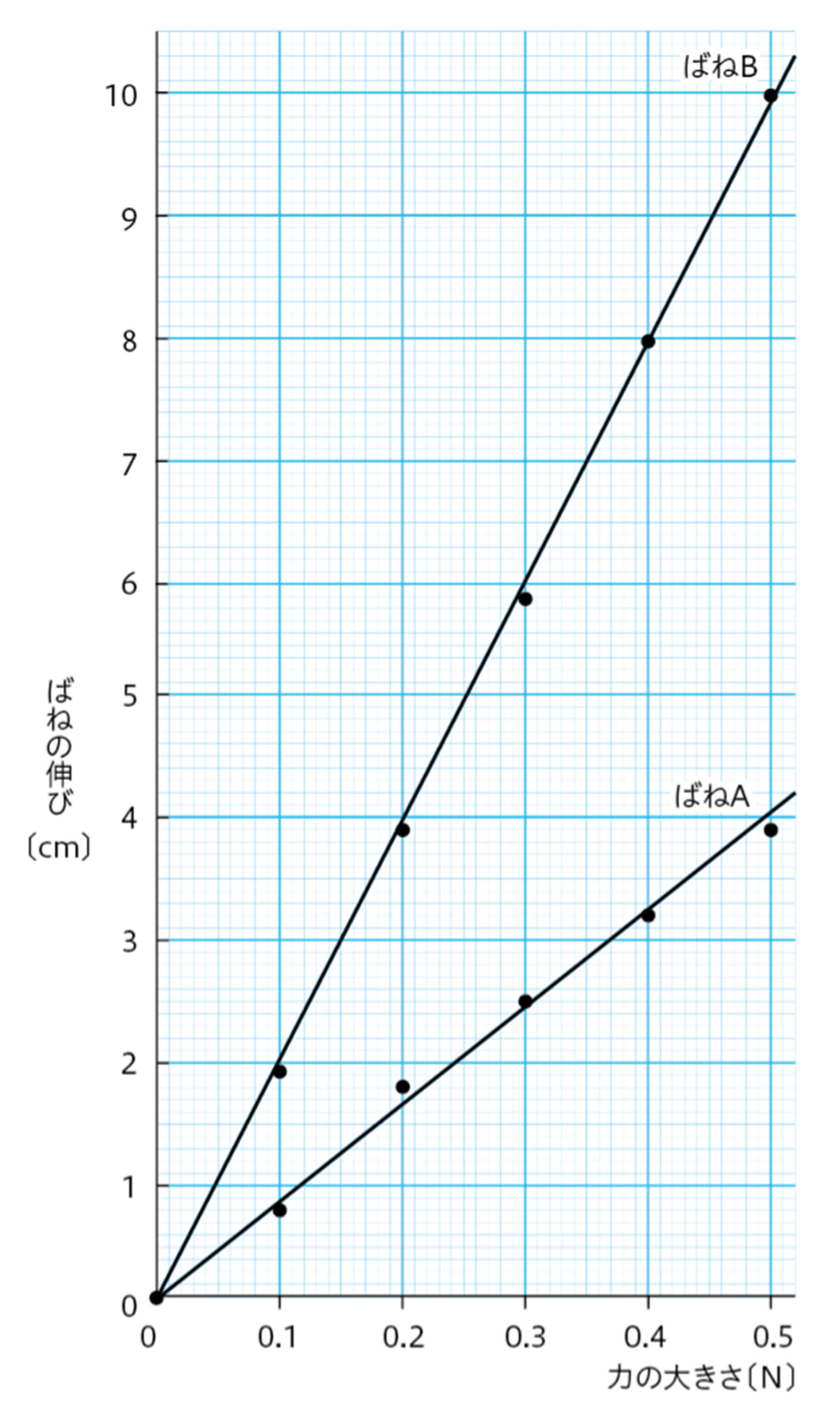
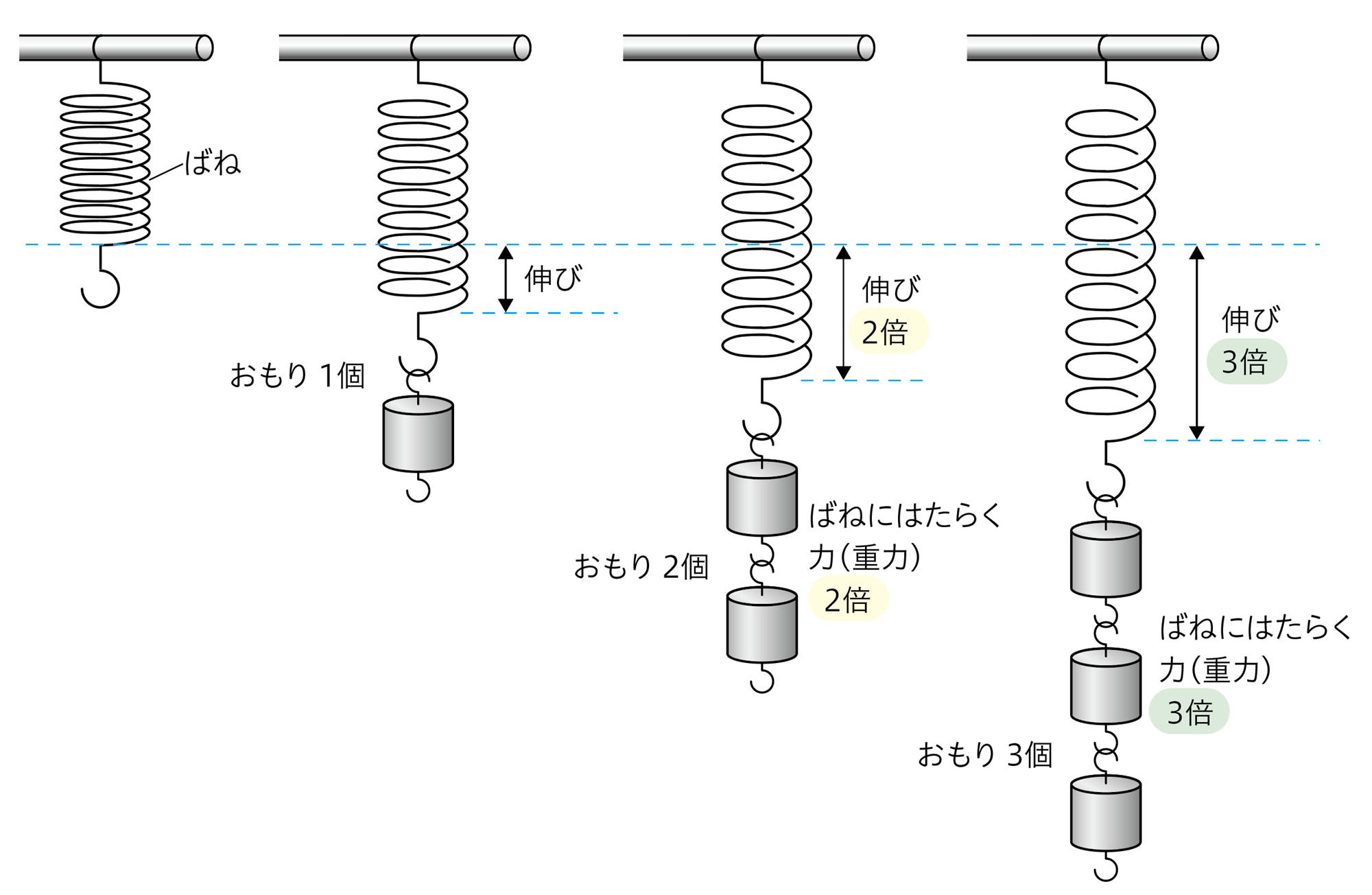
- 探究7の結果をグラフに表すと，図9のような直線になる。このグラフは，横軸の値（力の大きさ）が2倍，3倍になると，縦軸の値（ばねの伸び）も2倍，3倍となっており，比例の関係を表している。つまり，ばねの伸びは，ばねにはたらく力の大きさに比例する。
- ばねAとばねBは，同じ重力による伸びの量が異なり，ばねによって，比例定数は異なると考えられる。
※このウェブページは中学校理科１年の学習内容です。<1年p.137>
ばねの伸びは，ばねにはたらく力の大きさに比例❶する。この関係は【フックの法則】❷とよばれる。ばねばかりは，フックの法則を利用してつくられている❸（図10）。
５ 力を表す矢印
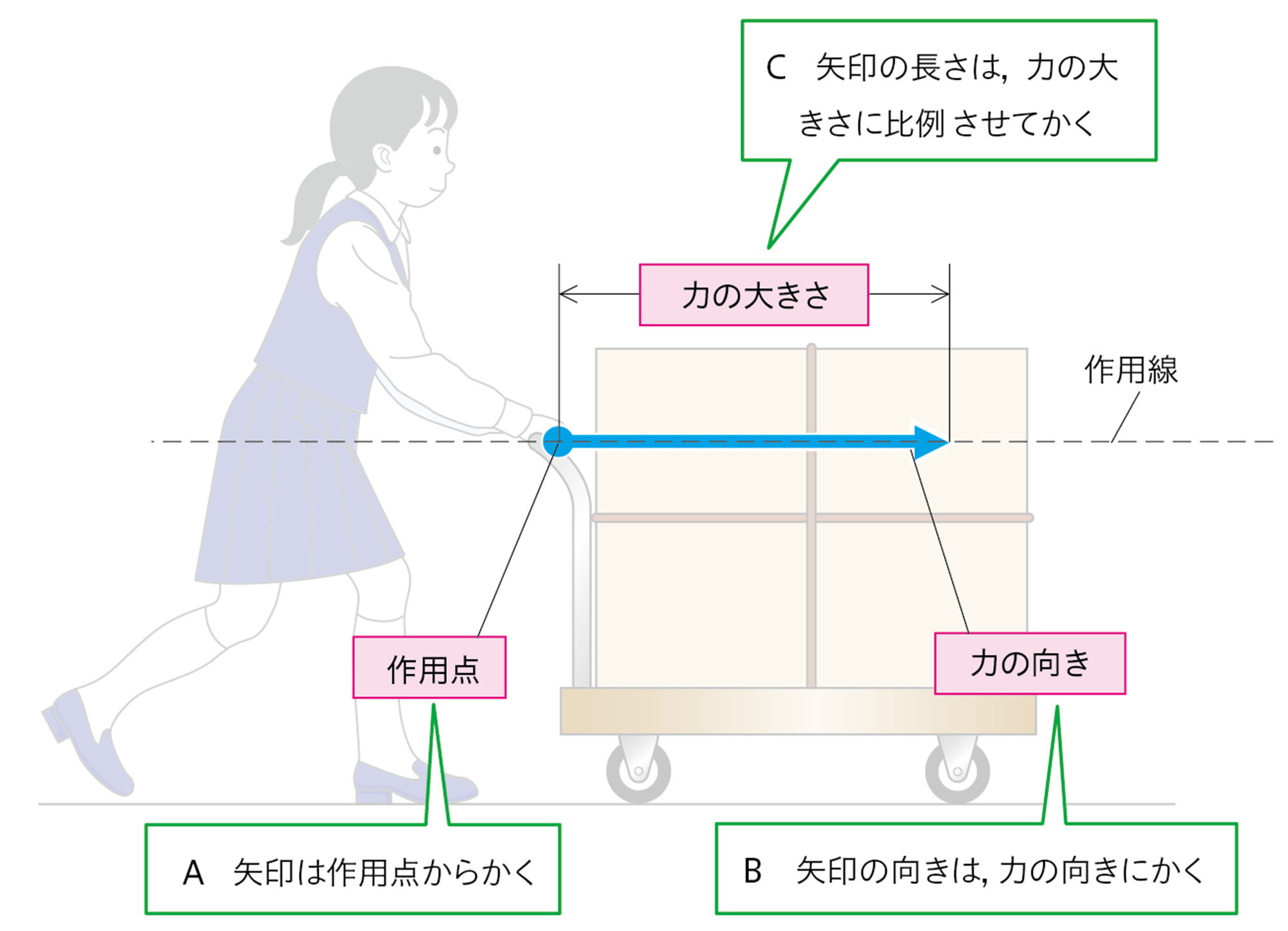
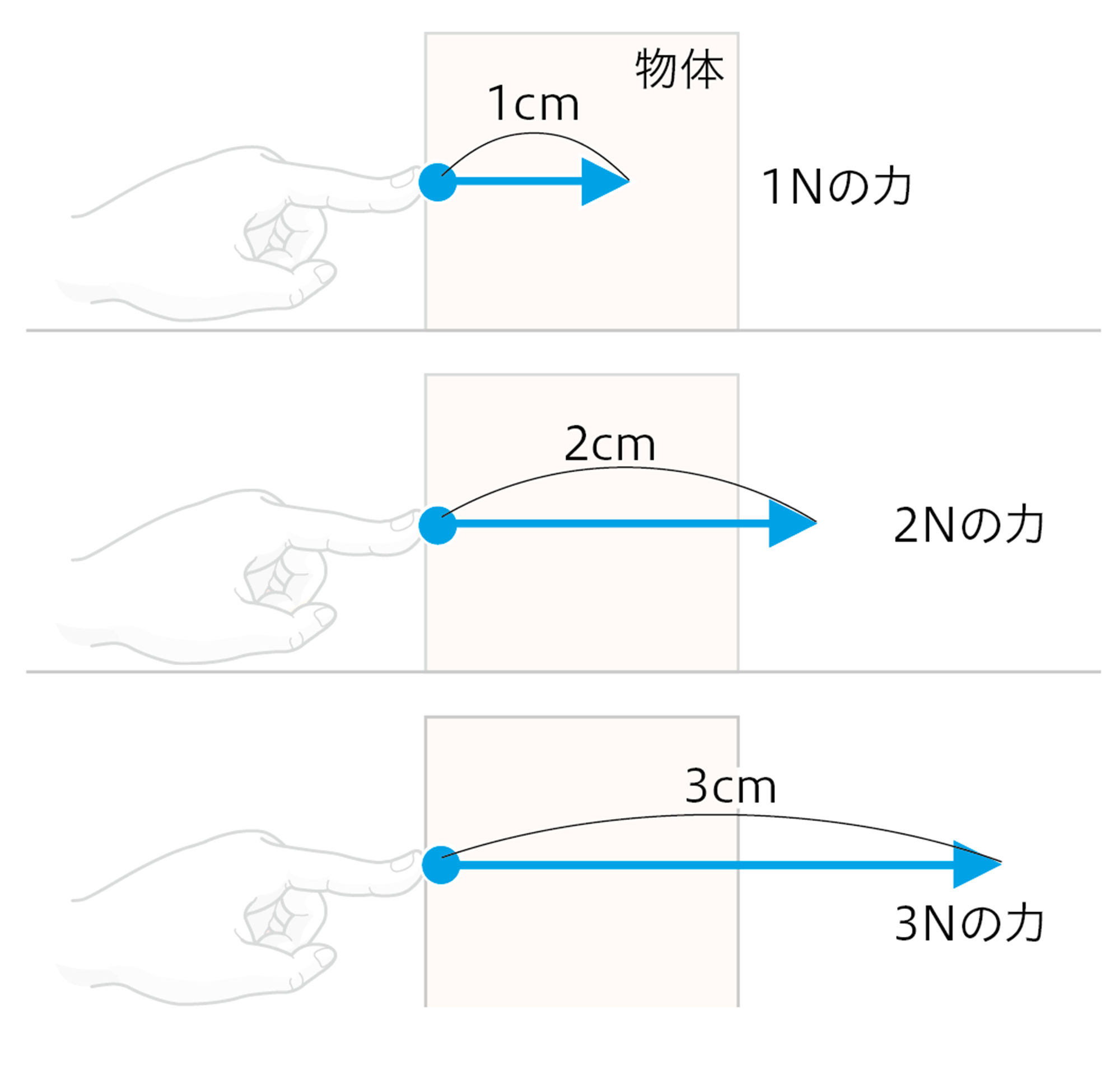
物体に力がはたらくとき，「どのくらいの力」が，「どの向き」に，「物体のどの場所から」はたらくかによって，物体の動きが異なる。このような力のはたらきを表すときは，力の矢印を用いるとわかりやすい。
このとき，図11のように
「物体のどの場所から」は，【A 力のはたらく点（作用点）】
「どの向き」は，【B 力の向き】，
「どのくらいの力」は，【C 力の大きさ】，
として表すことに注意する。
力のはたらきが異なることを，力の矢印でうまく表せるかな。
❶ 比例とは，ある量が2倍，3倍と変化するとき，もう1つの量も2倍，3倍と変化する関係をいう。
❷ フックの法則は，イギリスの科学者フック（1635〜1703年）の名からつけられた。フックは，光や力，惑星の運動などの研究で功績を残した。
❸ フックの法則は，ばねだけでなく，ゴムひもなど変形するともとにもどろうとする力（弾性力）をもつ物体に広く見られる法則であることが知られている。
※このウェブページは中学校理科１年の学習内容です。<1年p.138>
力の矢印をかくとき，右の①〜⑤の順番で考えていくとわかりやすい。なお，重力の作用点は，物体の中心として表す。それ以外の場合は，「どこに」力がはたらいているのかに注意する（図13，14）。
① 力が「何（物体）」から「何（物体）」の「どこ」にはたらいているか，はっきり決める。
② ①をもとに作用点を決め，●.ではっきりと示す。
③ 物体に力がはたらく向きに力の矢印をのばす。
④ １Nを何cmとして矢印をえがくか決めておき，力の大きさに比例させて，矢印の長さを調節する。
１Nを何cmにするか，基準となる長さは自分で決めます。
力を矢印で表すときは，基準が必要である。
たとえば1N の力を1cm の矢印で表すと決める。
重力の向き：「地球」が，物体を「地球の中心の方向（鉛直方向）」に引いている。
重力の作用点：物体の中心に作用点を打つ。
重力以外の力の向き：力がはたらく向きは，場合によって異なる。
力の作用点：「力がはたらく物体」のやや内側，面全体の中央に作用点を打つ。
重力以外の力は「力がはたらく場所」を意識しましょう。なお，ここでは，力が「物体に対してはたらく」ことを強調するため，作用点は「力がはたらく対象の物体」のやや内側に打っています。
作用点を打つ場所は，「何から」「何の」「どこ」に力がはたらくと考えるかによって変わります。
実際には，重力や物体を押す力は物体全体にはたらいています。
ただし，力の矢印は，図13のように１本にします。
ニュース
※科学ニュースの更新は2025年4月を目処にはじまります。
- 【フォークボールの落ちる謎をスパコンで解明：九州大学】 2023年3月1日フォークボールはバックスピンの回転をしているため，回転により浮き上がる力（揚力）を受けて上向きに曲がる軌道になるはずです。しかし，実際には放物線のような「落ちる」軌道を描きます。 このことは長らく謎とされてきましたが，ボールの縫い目まで詳細に計算する数値流体シミュレーションを実施したところ，ボールの縫い目の特定の角度において下向きの力「負のマグヌス効果」が生じ，ボールが落ちることが分かりました。 もと記事リンク 論文